题目内容
函数f(x)=ln(x+
)的图象是( )
| 1 |
| x |
A、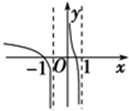 |
B、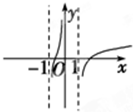 |
C、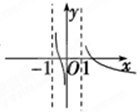 |
D、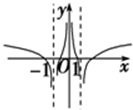 |
考点:函数的图象
专题:函数的性质及应用
分析:首先根据对数函数的性质,求出函数的定义域,再很据复合函数的单调性求出f(x)的单调性,问题得以解决.
解答:
解:因为x-
>0,解得x>1或-1<x<0,
所以函数f(x)=ln(x-
)的定义域为:(-1,0)∪(1,+∞).
所以选项A、D不正确.
当x∈(-1,0)时,g(x)=x-
是增函数,
因为y=lnx是增函数,所以函数f(x)=ln(x+
)是增函数.
故选B.
| 1 |
| x |
所以函数f(x)=ln(x-
| 1 |
| x |
所以选项A、D不正确.
当x∈(-1,0)时,g(x)=x-
| 1 |
| x |
因为y=lnx是增函数,所以函数f(x)=ln(x+
| 1 |
| x |
故选B.
点评:本题主要考查了对数函数的定义域和复合函数的单调性,属于基础题.

练习册系列答案
相关题目
A、B两位同学各有3张卡片,现以投掷硬币的形式进行游戏.当硬币正面向上时,A赢得B一张卡片,否则B赢得A一张卡片,如果某人已赢得所有卡片,则游戏终止,那么恰好掷完5次硬币时游戏终止的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
从正六边形六个顶点及其中心这7个点中,任取两个点,则这两个点的距离大于该正六边形边长的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|