题目内容
A、B两位同学各有3张卡片,现以投掷硬币的形式进行游戏.当硬币正面向上时,A赢得B一张卡片,否则B赢得A一张卡片,如果某人已赢得所有卡片,则游戏终止,那么恰好掷完5次硬币时游戏终止的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:列举法计算基本事件数及事件发生的概率
专题:计算题,概率与统计
分析:假设A赢了B,5次终止,那么A赢了4次,B赢了1次,结合每种情况概率均为(
)5,且还有B赢A的情况,即可得出结论.
| 1 |
| 2 |
解答:
解:假设A赢了B,5次终止,那么A赢了4次,B赢了1次. B的这一次只能发生在前三次中(前三中还不发生,A就赢了),也就是有三种情况,每种情况概率均为(
)5,且还有B赢A的情况,则最后概率为(
)5×3×2=
.
故选:D.
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 16 |
故选:D.
点评:本题考查概率的计算,考查学生分析解决问题的能力,比较基础.

练习册系列答案
相关题目
已知复数
•i2016(i是虚数单位)为纯虚数,则实数a的值为( )
| a+i |
| 1-2i |
| A、2 | B、2 | C、1 | D、-1 |
已知f(x)=
,则f(3)为( )
|
| A、2 | B、3 | C、4 | D、5 |
函数f(x)=ln(x+
)的图象是( )
| 1 |
| x |
A、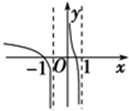 |
B、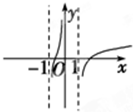 |
C、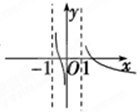 |
D、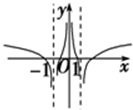 |
用平行于圆锥底面的平面截圆锥,所得截面面积与底面面积的比是1:3,这截面把圆锥母线分成的两段的比是( )
| A、1:3 | ||
B、1:(
| ||
| C、1:9 | ||
D、
|