题目内容
已知函数f(x)=3-4x,g(x)=2x+1,H(x)=f(x)+g(x),x∈R.
(1)设函数M(x)=
,求M(x)的最大值;
(2)判断H(x)的单调性,并用定义证明你的结论;
(3)当x∈[a,a+1](a∈R)时,求H(x)的最大值.
(1)设函数M(x)=
| H(x)-|f(x)-g(x)| |
| 2 |
(2)判断H(x)的单调性,并用定义证明你的结论;
(3)当x∈[a,a+1](a∈R)时,求H(x)的最大值.
考点:函数的最值及其几何意义,函数单调性的判断与证明
专题:证明题,分类讨论,函数的性质及应用
分析:(1)先求M(x)的解析式,再由M(x)的单调性,求出最大值;
(2)运用单调性的定义,在R上任取两数x1<x2,判断f(x1)-f(x2)与0的大小,判断函数的单调性;
(3)对a进行讨论,属于对称轴定区间动的情形,分三种情况.
(2)运用单调性的定义,在R上任取两数x1<x2,判断f(x1)-f(x2)与0的大小,判断函数的单调性;
(3)对a进行讨论,属于对称轴定区间动的情形,分三种情况.
解答:
解:(1)f(x)-g(x)=3-4x-2x+1=-(2x)2-2×2x+3=-(2x-1)(2x+3)
令f(x)-g(x)≥0得x≤0,由f(x)-g(x)<0得x>0,
M(x)=
,当x≤0时,M(x)=g(x)=2x+1≤2,
当x>0,M(x)=f(x)=3-4x<2,
∴M(x)的最大值为2.
(2)H(x)=3-4x+2x+1=-4x+2×2x+3,
任取x1,x2∈R,且x1<x2,
H(x1)-H(x2)=-4x1+2×2x1+3-(-4x2+2×2x2+3)=(2x2-2x1)(2x2+2x1-2)
∵2x2-2x1>0,
当x1<x2<0时,2x2+2x1-2<0,f(x1)-f(x2)<0,∴f(x)在(-∞,0)上单调递增,
当x2>x1>0时,2x2+2x1-2>0,∴f(x)在(0,+∞)上单调递减;
(3))H(x)=-4x+2×2x+3,
令t=2x,∵x∈[a,a+1],∴t∈[2a,2a+1],t>0,
∴y=-t2+2t+3=-(t-1)2+4,当t∈(0,1)时y单调递减,当t∈(1,+∞)时单调递增,
由(2)知当a≥0即t≥1时,H(x)单调递减,∴当t=2a时,有最大值,且最大值为H(a)=-4a+2a+1+3;
当a≤-1时即t+1≤1时,H(x)单调递增,∴当t=2a+1时,有最大值,且最大值为H(a+1)=-4a+1+2a+2+3;
当-1<a<0即
<t<2,H(x)在(
,1)单调递增,在(1,2)上单调递减,当t=1时有最大值,且最大值为H(1)=4.
令f(x)-g(x)≥0得x≤0,由f(x)-g(x)<0得x>0,
M(x)=
|
当x>0,M(x)=f(x)=3-4x<2,
∴M(x)的最大值为2.
(2)H(x)=3-4x+2x+1=-4x+2×2x+3,
任取x1,x2∈R,且x1<x2,
H(x1)-H(x2)=-4x1+2×2x1+3-(-4x2+2×2x2+3)=(2x2-2x1)(2x2+2x1-2)
∵2x2-2x1>0,
当x1<x2<0时,2x2+2x1-2<0,f(x1)-f(x2)<0,∴f(x)在(-∞,0)上单调递增,
当x2>x1>0时,2x2+2x1-2>0,∴f(x)在(0,+∞)上单调递减;
(3))H(x)=-4x+2×2x+3,
令t=2x,∵x∈[a,a+1],∴t∈[2a,2a+1],t>0,
∴y=-t2+2t+3=-(t-1)2+4,当t∈(0,1)时y单调递减,当t∈(1,+∞)时单调递增,
由(2)知当a≥0即t≥1时,H(x)单调递减,∴当t=2a时,有最大值,且最大值为H(a)=-4a+2a+1+3;
当a≤-1时即t+1≤1时,H(x)单调递增,∴当t=2a+1时,有最大值,且最大值为H(a+1)=-4a+1+2a+2+3;
当-1<a<0即
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查函数的单调性,最值,复合函数单调性,注意复合函数单调性的性质,属于中档题.

练习册系列答案
相关题目
已知f(x)=
,则f(3)为( )
|
| A、2 | B、3 | C、4 | D、5 |
函数f(x)=ln(x+
)的图象是( )
| 1 |
| x |
A、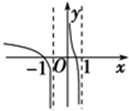 |
B、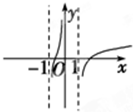 |
C、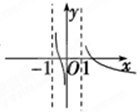 |
D、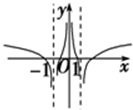 |
用平行于圆锥底面的平面截圆锥,所得截面面积与底面面积的比是1:3,这截面把圆锥母线分成的两段的比是( )
| A、1:3 | ||
B、1:(
| ||
| C、1:9 | ||
D、
|