题目内容
若函数f(x)为R上的减函数,且f(x)的图象经过点A(0,3)和B(3,-1),则不等式-1≤f(2x-1)≤3的解集为 .
考点:函数单调性的性质
专题:函数的性质及应用
分析:由已知条件知:f(0)=3,f(3)=-1,所以原不等式变成:f(3)≤f(2x-1)≤f(0),根据f(x)在R上是减函数得到,3≤2x-1≤0,解该不等式即得原不等式的解集.
解答:
解:f(x)的图象经过点A(0,3),B(3,-1),则:
f(0)=3,f(3)=-1;
∴由原不等式得:f(3)≤f(2x-1)≤f(0);
∵f(x)是R上的减函数,所以:3≥2x-1≥0,解得
≤x≤2;
∴原不等式的解集为[
,2].
故答案为:[
,2].
f(0)=3,f(3)=-1;
∴由原不等式得:f(3)≤f(2x-1)≤f(0);
∵f(x)是R上的减函数,所以:3≥2x-1≥0,解得
| 1 |
| 2 |
∴原不等式的解集为[
| 1 |
| 2 |
故答案为:[
| 1 |
| 2 |
点评:考查函数解析式和该函数图象上点的坐标的关系,以及减函数的定义.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数f(x)=ln(x+
)的图象是( )
| 1 |
| x |
A、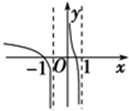 |
B、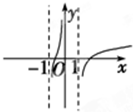 |
C、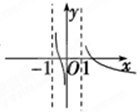 |
D、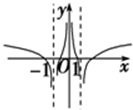 |
用平行于圆锥底面的平面截圆锥,所得截面面积与底面面积的比是1:3,这截面把圆锥母线分成的两段的比是( )
| A、1:3 | ||
B、1:(
| ||
| C、1:9 | ||
D、
|
设f(x)是定义在R上的奇函数,且f(2)=0,当x>0时,有
>0恒成立,则不等式f(x)>0的解集是( )
| xf′(x)-f(x) |
| x2 |
| A、(-∞,-2)∪(2,+∞) |
| B、(-2,0)∪(0,2) |
| C、(-2,0)∪(2,+∞) |
| D、(-∞,-2)∪(0,2) |
 如图,△ABC内接于⊙O,AB是⊙O的不是直径的弦,∠CAD=∠ABC,判断直线AD与⊙O的位置关系,并说明理由.
如图,△ABC内接于⊙O,AB是⊙O的不是直径的弦,∠CAD=∠ABC,判断直线AD与⊙O的位置关系,并说明理由.