题目内容
已知圆锥的母线长为3cm,底面半径为1cm,圆锥顶点为P,底面圆周上有一点A,由A点出发绕圆锥侧面一周.
(1)回到A点的最短距离为多少?
(2)到达AP中点的最短距离为多少?
(1)回到A点的最短距离为多少?
(2)到达AP中点的最短距离为多少?
考点:点、线、面间的距离计算
专题:空间位置关系与距离
分析:(1)圆锥的侧面展开图是扇形,从A点出发绕侧面一周,再回到A点的最短的路线即展开得到的扇形的弧所对弦,转化为求弦长的问题.
(2)AP中点的最短距离即OH.
(2)AP中点的最短距离即OH.
解答:
解:(1)圆锥的侧面展开图是扇形,从A点出发绕侧面一周,
再回到A点的最短的路线即展开得到的扇形的弧所对弦,
转化为求弦长的问题
如图所示,设展开的扇形的圆心角为α
∵圆锥底面半径r=1cm,母线长是OA=3cm,
∴根据弧长公式得到2π×1=α×3,
∴α=
,即扇形的圆心角是
,
∴∠AOH=60°
∴动点P自A出发在侧面上绕一周到A点的最短路程为弧所对的弦长:
AA′=2AH=2×OAsin∠AOH=2×3×
=3
.
(2)AP中点的最短距离即OH
∴OH=OAcos60°=
.
再回到A点的最短的路线即展开得到的扇形的弧所对弦,
转化为求弦长的问题
如图所示,设展开的扇形的圆心角为α
∵圆锥底面半径r=1cm,母线长是OA=3cm,

∴根据弧长公式得到2π×1=α×3,
∴α=
| 2 |
| 3 |
| 2 |
| 3 |
∴∠AOH=60°
∴动点P自A出发在侧面上绕一周到A点的最短路程为弧所对的弦长:
AA′=2AH=2×OAsin∠AOH=2×3×
| ||
| 2 |
| 3 |
(2)AP中点的最短距离即OH
∴OH=OAcos60°=
| 3 |
| 2 |
点评:本题考查最短距离的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
已知复数
•i2016(i是虚数单位)为纯虚数,则实数a的值为( )
| a+i |
| 1-2i |
| A、2 | B、2 | C、1 | D、-1 |
已知f(x)=
,则f(3)为( )
|
| A、2 | B、3 | C、4 | D、5 |
函数f(x)=ln(x+
)的图象是( )
| 1 |
| x |
A、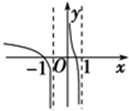 |
B、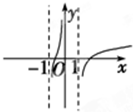 |
C、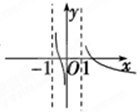 |
D、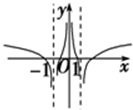 |