题目内容
设0<θ<
,向量
=(sin2θ,cosθ),
=(1,-cosθ),若
•
=0,则tanθ= .
| π |
| 2 |
| a |
| b |
| a |
| b |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:由条件利用两个向量的数量积公式求得 2sinθcosθ-cos2θ=0,再利用同角三角函数的基本关系求得tanθ
解答:
解:∵
•
=sin2θ-cos2θ=2sinθcosθ-cos2θ=0,0<θ<
,
∴2sinθ-cosθ=0,∴tanθ=
,
故答案为:
.
| a |
| b |
| π |
| 2 |
∴2sinθ-cosθ=0,∴tanθ=
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题主要考查两个向量的数量积公式,同角三角函数的基本关系,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设函数f(x)=x3-4x+a(a>0),若f(x)的三个零点分别为x1,x2,x3,且x1<x2<x3,则( )
| A、x1>-2 | ||
B、x12+x22<
| ||
| C、x3>2 | ||
D、x22+x32<
|
已知双曲线C的离心率为2,焦点为F1、F2,点A在C上,若|F1A|=2|F2A|,则cos∠AF2F1=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图1,四面体ABCD及其三视图(如图2所示),过棱AB的中点E作平行于AD,BC的平面分别交四面体的棱BD,DC,CA于点F,G,H.
如图1,四面体ABCD及其三视图(如图2所示),过棱AB的中点E作平行于AD,BC的平面分别交四面体的棱BD,DC,CA于点F,G,H.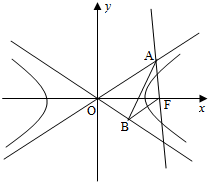 如图,已知双曲线C:
如图,已知双曲线C: