题目内容
设{an}是公比为q的等比数列,则“q>1”是“{an}”为递增数列的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断,等比数列
专题:等差数列与等比数列,简易逻辑
分析:根据等比数列的性质,结合充分条件和必要条件的定义进行判断即可得到结论.
解答:
解:等比数列-1,-2,-4,…,满足公比q=2>1,但“{an}”不是递增数列,充分性不成立.
若an=-1•(
)n-1为递增数列,但q=
>1不成立,即必要性不成立,
故“q>1”是“{an}”为递增数列的既不充分也不必要条件,
故选:D.
若an=-1•(
| 1 |
| 2 |
| 1 |
| 2 |
故“q>1”是“{an}”为递增数列的既不充分也不必要条件,
故选:D.
点评:本题主要考查充分条件和必要条件的判断,利用等比数列的性质,利用特殊值法是解决本题的关键.

练习册系列答案
相关题目
设
,
,
是非零向量,已知命题p:若
•
=0,
•
=0,则
•
=0;命题q:若
∥
,
∥
,则
∥
,则下列命题中真命题是( )
| a |
| b |
| c |
| a |
| b |
| b |
| c |
| a |
| c |
| a |
| b |
| b |
| c |
| a |
| c |
| A、p∨q |
| B、p∧q |
| C、(¬p)∧(¬q) |
| D、p∨(¬q) |
在“世界读书日”前夕,为了了解某地5000名居民某天的阅读时间,从中抽取了200名居民的阅读时间进行统计分析,在这个问题中,5000名居民的阅读时间的全体是( )
| A、总体 |
| B、个体 |
| C、样本的容量 |
| D、从总体中抽取的一个样本 |
已知双曲线C的离心率为2,焦点为F1、F2,点A在C上,若|F1A|=2|F2A|,则cos∠AF2F1=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
直线l:y=kx+1与圆O:x2+y2=1相交于A,B 两点,则“k=1”是“△OAB的面积为
”的( )
| 1 |
| 2 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
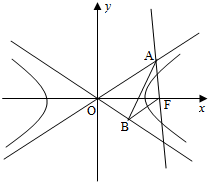 如图,已知双曲线C:
如图,已知双曲线C: