题目内容
已知{an}是等差数列,满足a1=3,a4=12,数列{bn}满足b1=4,b4=20,且{bn-an}为等比数列.
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)求数列{bn}的前n项和.
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)求数列{bn}的前n项和.
考点:数列的求和,等差数列的通项公式,等比数列的通项公式
专题:等差数列与等比数列
分析:(Ⅰ)利用等差数列、等比数列的通项公式先求得公差和公比,即得结论;
(Ⅱ)利用分组求和法,有等差数列及等比数列的前n项和公式即可求得数列的和.
(Ⅱ)利用分组求和法,有等差数列及等比数列的前n项和公式即可求得数列的和.
解答:
解:(Ⅰ)设等差数列{an}的公差为d,由题意得
d=
=
=3.
∴an=a1+(n-1)d=3n(n=1,2,…),
设等比数列{bn-an}的公比为q,则
q3=
=
=8,∴q=2,
∴bn-an=(b1-a1)qn-1=2n-1,
∴bn=3n+2n-1(n=1,2,…).
(Ⅱ)由(Ⅰ)知bn=3n+2n-1(n=1,2,…).
∵数列{an}的前n项和为
n(n+1),数列{2n-1}的前n项和为1×
=2n-1,
∴数列{bn}的前n项和为
n(n+1)+2n-1.
d=
| a4-a1 |
| 3 |
| 12-3 |
| 3 |
∴an=a1+(n-1)d=3n(n=1,2,…),
设等比数列{bn-an}的公比为q,则
q3=
| b4-a4 |
| b1-a1 |
| 20-12 |
| 4-3 |
∴bn-an=(b1-a1)qn-1=2n-1,
∴bn=3n+2n-1(n=1,2,…).
(Ⅱ)由(Ⅰ)知bn=3n+2n-1(n=1,2,…).
∵数列{an}的前n项和为
| 3 |
| 2 |
| 1-2n |
| 1-2 |
∴数列{bn}的前n项和为
| 3 |
| 2 |
点评:本题主要考查学生对等差数列及等比数列的通项公式和前n项和公式的应用,考查学生的基本的运算能力,属基础题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
已知六张卡片中,三张红色,三张黑色,它们分别标有数字2,3,4,打乱后分给甲,乙,丙三人,每人两张,若两张卡片所标数字相同称为“一对”卡片,则三人中至少有一人拿到“一对”卡片的分法数为( )
| A、18 | B、24 | C、42 | D、48 |
设
,
,
是非零向量,已知命题p:若
•
=0,
•
=0,则
•
=0;命题q:若
∥
,
∥
,则
∥
,则下列命题中真命题是( )
| a |
| b |
| c |
| a |
| b |
| b |
| c |
| a |
| c |
| a |
| b |
| b |
| c |
| a |
| c |
| A、p∨q |
| B、p∧q |
| C、(¬p)∧(¬q) |
| D、p∨(¬q) |
 如图,已知两条抛物线E1:y2=2p1x(p1>0)和E2:y2=2p2x(p2>0),过原点O的两条直线l1和l2,l1与E1,E2分别交于A1、A2两点,l2与E1、E2分别交于B1、B2两点.
如图,已知两条抛物线E1:y2=2p1x(p1>0)和E2:y2=2p2x(p2>0),过原点O的两条直线l1和l2,l1与E1,E2分别交于A1、A2两点,l2与E1、E2分别交于B1、B2两点. 如图1,四面体ABCD及其三视图(如图2所示),过棱AB的中点E作平行于AD,BC的平面分别交四面体的棱BD,DC,CA于点F,G,H.
如图1,四面体ABCD及其三视图(如图2所示),过棱AB的中点E作平行于AD,BC的平面分别交四面体的棱BD,DC,CA于点F,G,H.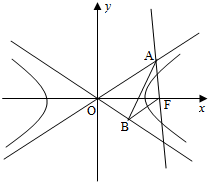 如图,已知双曲线C:
如图,已知双曲线C: