题目内容
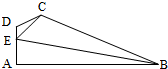 如图,在平面四边形ABCD中,DA⊥AB,DE=1,EC=
如图,在平面四边形ABCD中,DA⊥AB,DE=1,EC=| 7 |
| 2π |
| 3 |
| π |
| 3 |
(Ⅰ)求sin∠CED的值;
(Ⅱ)求BE的长.
考点:余弦定理的应用,正弦定理
专题:解三角形
分析:(Ⅰ)根据三角形边角之间的关系,结合正弦定理和余弦定理即可得到结论.
(Ⅱ)利用两角和的余弦公式,结合正弦定理即可得到结论.
(Ⅱ)利用两角和的余弦公式,结合正弦定理即可得到结论.
解答:
解:(Ⅰ)设α=∠CED,
在△CDE中,由余弦定理得EC2=CD2+ED2-2CD•DEcos∠CDE,
即7=CD2+1+CD,则CD2+CD-6=0,
解得CD=2或CD=-3,(舍去),
在△CDE中,由正弦定理得
=
,
则sinα=
=
=
,
即sin∠CED=
.
(Ⅱ)由题设知0<α<
,由(Ⅰ)知cosα=
=
=
,
而∠AEB=
-α,
∴cos∠AEB=cos(
-α)=cos
cosα+sin
sinα=-
×
+
×
=
,
在Rt△EAB中,cos∠AEB=
=
,
故BE=
=
=4
.
在△CDE中,由余弦定理得EC2=CD2+ED2-2CD•DEcos∠CDE,
即7=CD2+1+CD,则CD2+CD-6=0,
解得CD=2或CD=-3,(舍去),
在△CDE中,由正弦定理得
| EC |
| sin∠EDC |
| CD |
| sinα |
则sinα=
CD•sin
| ||
| EC |
2×
| ||||
|
| ||
| 7 |
即sin∠CED=
| ||
| 7 |
(Ⅱ)由题设知0<α<
| π |
| 3 |
| 1-sin2α |
1-
|
2
| ||
| 7 |
而∠AEB=
| 2π |
| 3 |
∴cos∠AEB=cos(
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| 1 |
| 2 |
2
| ||
| 7 |
| ||
| 2 |
| ||
| 7 |
| ||
| 14 |
在Rt△EAB中,cos∠AEB=
| EA |
| BE |
| 2 |
| BE |
故BE=
| 2 |
| cos∠AEB |
| 2 | ||||
|
| 7 |
点评:本题主要考查解三角形的应用,根据正弦定理和余弦定理是解决本题本题的关键,难度不大.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
下列各组函数y=f(x)与y=g(x)在交点处有共同切线的是( )
①f(x)=x2-1,g(x)=lnx
②f(x)=3x2+1,g(x)=x3+3x
③f(x)=(x+1)2,g(x)=ex
④f(x)=
,g(x)=
lnx.
①f(x)=x2-1,g(x)=lnx
②f(x)=3x2+1,g(x)=x3+3x
③f(x)=(x+1)2,g(x)=ex
④f(x)=
| x |
| e |
| 2 |
| A、①② | B、②④ | C、②③ | D、③④ |
在“世界读书日”前夕,为了了解某地5000名居民某天的阅读时间,从中抽取了200名居民的阅读时间进行统计分析,在这个问题中,5000名居民的阅读时间的全体是( )
| A、总体 |
| B、个体 |
| C、样本的容量 |
| D、从总体中抽取的一个样本 |
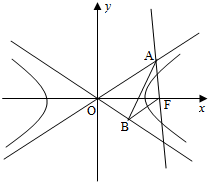 如图,已知双曲线C:
如图,已知双曲线C: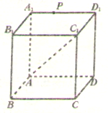 如图,P是正方体ABCD-A1B1C1D1上一动点,设点P和直线AC1确定的平面为α,过点P与直线AC1垂直的平面为β,则下列命题正确的序号是
如图,P是正方体ABCD-A1B1C1D1上一动点,设点P和直线AC1确定的平面为α,过点P与直线AC1垂直的平面为β,则下列命题正确的序号是