题目内容
若f（x）=ln（e3x+1）+ax是偶函数，则a= ．
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：根据函数奇偶性的定义，建立方程关系即可得到结论．
解答：
解：若f（x）=ln（e3x+1）+ax是偶函数，
则f（-x）=f（x），
即ln（e3x+1）+ax=ln（e-3x+1）-ax，
即2ax=ln（e-3x+1）-ln（e3x+1）=ln(
)=lne-3x=-3x，
即2a=-3，解得a=-
，
故答案为：-
，
则f（-x）=f（x），
即ln（e3x+1）+ax=ln（e-3x+1）-ax，
即2ax=ln（e-3x+1）-ln（e3x+1）=ln(
| e-3x+1 |
| e3x+1 |
即2a=-3，解得a=-
| 3 |
| 2 |
故答案为：-
| 3 |
| 2 |
点评：本题主要考查函数奇偶性的应用，根据偶函数的定义得到f（-x）=f（x）是解决本题的关键．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
如图，已知两条抛物线E1：y2=2p1x（p1＞0）和E2：y2=2p2x（p2＞0），过原点O的两条直线l1和l2，l1与E1，E2分别交于A1、A2两点，l2与E1、E2分别交于B1、B2两点．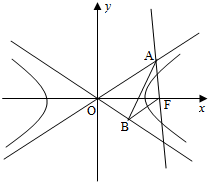
如图，已知双曲线C：
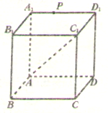如图，P是正方体ABCD-A1B1C1D1上一动点，设点P和直线AC1确定的平面为α，过点P与直线AC1垂直的平面为β，则下列命题正确的序号是
设
，
，
是非零向量，已知命题p：若
•
=0，
•
=0，则
•
=0；命题q：若
∥
，
∥
，则
∥
，则下列命题中真命题是（ ）
| a |
| b |
| c |
| a |
| b |
| b |
| c |
| a |
| c |
| a |
| b |
| b |
| c |
| a |
| c |
| A、p∨q |
| B、p∧q |
| C、（￢p）∧（￢q） |
| D、p∨（￢q） |