题目内容
设不等式组
,表示的平面区域为Ω,在区域Ω内任取一点P(x,y),则P点的坐标满足不等式x2+y2≤2的概率为( )
|
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:简单线性规划,几何概型
专题:概率与统计
分析:由
我们易画出图象求出其对应的面积,即所有基本事件总数对应的几何量,再求出区域内和圆重合部分的面积,代入几何概型计算公式,即可得到答案.
|
解答:
 解:满足约束条件
解:满足约束条件
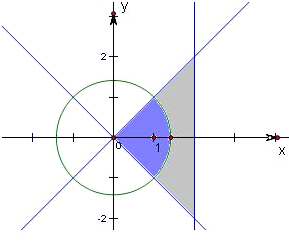
区域为△ABC内部(含边界),
与圆x2+y2=2的公共部分如图中阴影部分所示,
则点P落在圆x2+y2=2内的概率概率为P=
=
=
,
故选A.
 解:满足约束条件
解:满足约束条件
|
与圆x2+y2=2的公共部分如图中阴影部分所示,
则点P落在圆x2+y2=2内的概率概率为P=
| S扇形 |
| S三角形 |
| ||
|
| π |
| 8 |
故选A.
点评:本题考查的知识点是几何概型,二元一次不等式(组)与平面区域,求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据P=
求解.
| N(A) |
| N |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
复数(
)3的共轭复数为( )
| 1+i |
| 1-i |
| A、1 | B、-1 | C、i | D、-i |
二项式(2
-
)6的展开式的常数项是( )
| x |
| 1 | ||
2
|
| A、20 | B、-20 |
| C、15 | D、-15 |
i是虚数单位,
的共轭复数为( )
| 2i |
| 1-i |
| A、-1+i | B、1+i |
| C、-1-i | D、1-i |
若实数x,y满足
,则z=2x+2y的最小值是( )
|
| A、0 | ||
| B、1 | ||
C、
| ||
| D、9 |
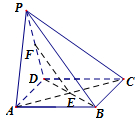 如图,已知四棱锥P-ABCD的底面为菱形,对角线AC与BD相交于点E,平面PAC垂直于底面ABCD,线段PD的中点为F.
如图,已知四棱锥P-ABCD的底面为菱形,对角线AC与BD相交于点E,平面PAC垂直于底面ABCD,线段PD的中点为F.