题目内容
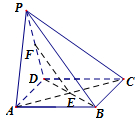如图，已知四棱锥P-ABCD的底面为菱形，对角线AC与BD相交于点E，平面PAC垂直于底面ABCD，线段PD的中点为F．（1）求证：EF∥平面PBC；
（2）求证：BD⊥PC．
考点：直线与平面平行的判定
专题：空间位置关系与距离
分析：（1）根据E，F为PD，DB的中点判断出EF为△PBD的中位线可知EF∥PB，进而根据EF?平面PBC，推断出EF平行于PB所在的平面PBC．
（2）先判断出BD⊥平面PAC，进而根据线面垂直的性质判断出BD⊥PC．
（2）先判断出BD⊥平面PAC，进而根据线面垂直的性质判断出BD⊥PC．
解答：
（1）证明：∵菱形对角线AC与BD相交于点E，
∴AC与BD互相平分，即AE=CE，BE=DE
又∵线段PD的中点为F，
∴EF为△PBD的中位线，
∴EF∥PB
又EF?平面PBC，PB?平面PBC，
∴EF∥平面PBC
（2）证明：∵平面PAC⊥底面ABCD，平面PAC∩底面ABCD=AC，
菱形ABCD中，AC⊥BD，BD?平面ABCD，
∴BD⊥平面PAC，
∴BD⊥PC．
∴AC与BD互相平分，即AE=CE，BE=DE
又∵线段PD的中点为F，
∴EF为△PBD的中位线，
∴EF∥PB
又EF?平面PBC，PB?平面PBC，
∴EF∥平面PBC
（2）证明：∵平面PAC⊥底面ABCD，平面PAC∩底面ABCD=AC，
菱形ABCD中，AC⊥BD，BD?平面ABCD，
∴BD⊥平面PAC，
∴BD⊥PC．
点评：本题主要考查了线面平行的判定，线面垂直的性质等知识．对线面平行的性质和判定定理即线面垂直性质和判定定理熟记于心，并能灵活运用．
练习册系列答案
相关题目
如果一个几何体的三视图如图所示（单位长度：cm），则此几何体的体积是（ ）A、
| ||
| B、64 | ||
C、
| ||
D、
|
设不等式组
，表示的平面区域为Ω，在区域Ω内任取一点P（x，y），则P点的坐标满足不等式x2+y2≤2的概率为（ ）
|
A、
| ||||
B、
| ||||
C、
| ||||
D、
|