题目内容
15.已知平面向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$=1|,$\overrightarrow{a}$•$\overrightarrow{b}$=1,|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{5}$,则|$\overrightarrow{b}$|=( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
分析 根据条件,对$|\overrightarrow{a}+\overrightarrow{b}|=\sqrt{5}$两边平方便可求出${\overrightarrow{b}}^{2}$的值,进而求出$|\overrightarrow{b}|$的值.
解答 解:根据条件,
$(\overrightarrow{a}+\overrightarrow{b})^{2}={\overrightarrow{a}}^{2}+2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}$=$1+2+{\overrightarrow{b}}^{2}=5$;
∴${\overrightarrow{b}}^{2}=2$;
∴$|\overrightarrow{b}|=\sqrt{2}$.
故选B.
点评 考查数量积的运算,以及数量积的计算公式.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
18.某三棱锥的三视图如图所示,则该三棱锥中最长棱的长度为( )
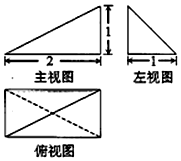

| A. | $\sqrt{5}$ | B. | $\sqrt{6}$ | C. | $2\sqrt{2}$ | D. | 3 |
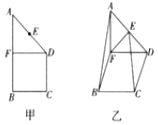 如图所示,在直角梯形ABCD中,AB∥CD,∠ABC=90°,CD=BC=1,点E为AD边上的中点,过点D作DF∥BC交AB于点F,现将此直角梯形沿DF折起,使得A-FD-B为直二面角,如图乙所示.
如图所示,在直角梯形ABCD中,AB∥CD,∠ABC=90°,CD=BC=1,点E为AD边上的中点,过点D作DF∥BC交AB于点F,现将此直角梯形沿DF折起,使得A-FD-B为直二面角,如图乙所示.