题目内容
6.设点$A(-2,\sqrt{3})$,B(2,0),点M在椭圆$\frac{x^2}{16}+\frac{y^2}{12}=1$上运动,当|MA|+|MB|最大时,点M的坐标为8+$\sqrt{3}$.分析 B为椭圆右焦点,设左焦点为F,则由椭圆定义|MA|+|MF|=2a,于是|MA|+|MB|=2a+|MA|-|MF|.有-|AF|<|MA|-|MF|<|BF|.显然当M在直线BF与椭圆第三象限交点时|MA|+|MB|有最大值.
解答 解:B为椭圆右焦点,设左焦点为F(-2,0),则由椭圆定义|MA|+|MF|=2a=8,
于是|MA|+|MB|=8+|MA|-|MF|.
当M不在直线AF与椭圆交点上时,M、F、A三点构成三角形,于是|MA|-|MF|<|BF|,
而当M在直线BF与椭圆交点上时,在第一象限交点时,有|MA|-|MF|=-|AF|,
在第三象限交点时有|MA|-|MF|=|BF|.
显然当M在直线BF与椭圆第三象限交点时|MA|+|MB|有最大值,
|MA|+|MB|=8+|MA|-|MF|=8+|AF|=8+$\sqrt{3}$
故答案为:8+$\sqrt{3}$
点评 本题考查椭圆的基本性质,转化思想是解题的关键,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.已知全集U=R,集合A={x|x2-x-6≤0},$B=\left\{{\left.x\right|\frac{4-x}{x+1}≤0}\right\}$,那么集合A∩(∁UB)=( )
| A. | [-2,4) | B. | (-1,3] | C. | [-2,-1] | D. | [-1,3] |
18.圆的一条直径的两个端点是(2,0),(0,2)时,则此圆的方程是( )
| A. | (x-2)2+(y-1)2=1 | B. | (x-1)2+(y-1)2=2 | C. | (x-1)2+(y+1)2=9 | D. | (x+2)2+(y+1)2=2 |
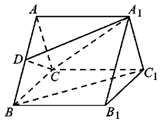 如图,在三棱柱ABC-A1B1C1中,底面△ABC是等边三角形,侧面AA1B1B为正方形,且AA1⊥平面ABC,D为线段AB上的一点.
如图,在三棱柱ABC-A1B1C1中,底面△ABC是等边三角形,侧面AA1B1B为正方形,且AA1⊥平面ABC,D为线段AB上的一点.