题目内容
7.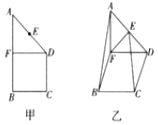 如图所示,在直角梯形ABCD中,AB∥CD,∠ABC=90°,CD=BC=1,点E为AD边上的中点,过点D作DF∥BC交AB于点F,现将此直角梯形沿DF折起,使得A-FD-B为直二面角,如图乙所示.
如图所示,在直角梯形ABCD中,AB∥CD,∠ABC=90°,CD=BC=1,点E为AD边上的中点,过点D作DF∥BC交AB于点F,现将此直角梯形沿DF折起,使得A-FD-B为直二面角,如图乙所示.(1)求证:AB∥平面CEF;
(2)若AF=$\sqrt{3}$,求点A到平面CEF的距离.
分析 (1)证明AB∥OE,即可得到AB∥平面CEF,
(2)如图5,连接FC,AC,取FD中点G,连接EG,CG.易得EG⊥平面BCEF,DC⊥平面ADF.由VA-CEF=VC-AEF,解得点A到平面CEF的距离
解答 解:(1)证明:如图4所示,连接BD,FC交于点O,连接OE.
因为BCDF为正方形,故O为BD中点.
又E为AD中点,故OE为△ADB的中位线. …(3分)
∵AB∥OE,又OE?平面CEF,AB?平面CEF,
∴AB∥平面CEF.…(5分)
(2)解:如图5,连接FC,AC,取FD中点G,连接EG,CG.
因为AF=$\sqrt{3}$,易得EF=$\frac{1}{2}AD=1$,EG=$\frac{1}{2}AF=\frac{\sqrt{3}}{2}$
∵GC=$\sqrt{{1}^{2}+(\frac{1}{2})^{2}}=\frac{\sqrt{3}}{2}$. …(7分)
因为原图形为直角梯形,折起后A-FD-B为直二面角,
故易得EG⊥平面BCEF,DC⊥平面ADF.
∴EC=$\sqrt{E{G}^{2}+C{G}^{2}}=\sqrt{(\frac{\sqrt{3}}{2})^{2}+(\frac{\sqrt{5}}{2})^{2}}=\sqrt{2}$..
又FC=$\sqrt{2}$,故易得等腰△CEF面积s△CFE=$\frac{\sqrt{7}}{4}$,
而s△AFE=$\frac{\sqrt{3}}{3}$.…(10分)
设点A到平面CEF的距离为h,
∵VA-CEF=VC-AEF,即$\frac{1}{3}×\frac{\sqrt{7}}{4}×h=\frac{1}{3}×\frac{\sqrt{3}}{4}×1$,解得h=$\frac{\sqrt{21}}{7}$.
所以点A到平面CEF的距离为$\frac{\sqrt{21}}{7}$.…(12分)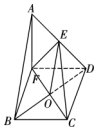
点评 本题考查了线面平行的判定,等体积法求点面距离,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | (x-2)2+(y-1)2=1 | B. | (x-1)2+(y-1)2=2 | C. | (x-1)2+(y+1)2=9 | D. | (x+2)2+(y+1)2=2 |
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
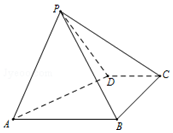 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,∠ABC=90°,AB∥CD,AB=AD=2,CD=1,侧面PAD⊥底面ABCD,且△PAD是以AD为底的等腰三角形
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,∠ABC=90°,AB∥CD,AB=AD=2,CD=1,侧面PAD⊥底面ABCD,且△PAD是以AD为底的等腰三角形