题目内容
20.新学年伊始,附中社团开始招新.某高一新生对“大观天文社”、“理科学社”、“水墨霓裳社”很感兴趣.假设他能被这三个社团接受的概率分别为$\frac{3}{4}$,$\frac{1}{2}$,$\frac{1}{3}$.(1)求此新生被两个社团接受的概率;
(2)设此新生最终参加的社团数为ξ,求ξ的分布列和数学期望.
分析 (1)设他被这三个社团接受分别是事件A,B,C.可得P=P(AB$\overline{C}$)+P(A$\overline{B}$C)+P($\overline{A}$BC).
(2)此新生参加的社团数ξ可能取值为0,1,2,3,利用相互独立与互斥事件的概率计算公式可得分布列与数学期望.
解答 解:(1)设他被这三个社团接受分别是事件A,B,C.
则P=P(AB$\overline{C}$)+P(A$\overline{B}$C)+P($\overline{A}$BC)=$\frac{3}{4}$×$\frac{1}{2}$×$\frac{2}{3}$+$\frac{3}{4}$×$\frac{1}{2}$×$\frac{1}{3}$+$\frac{1}{4}$×$\frac{1}{2}$×$\frac{1}{3}$=$\frac{5}{12}$.
(2)此新生参加的社团数ξ可能取值为0,1,2,3,
P(ξ=0)=$\frac{1}{4}$×$\frac{1}{2}$×$\frac{2}{3}$=$\frac{1}{12}$,P(ξ=1)=$\frac{3}{4}$×$\frac{1}{2}$×$\frac{2}{3}$+$\frac{1}{4}$×$\frac{1}{2}$×$\frac{1}{3}$+$\frac{1}{4}$×$\frac{1}{2}$×$\frac{2}{3}$=$\frac{3}{8}$,P(ξ=2)=$\frac{5}{12}$,
P(ξ=3)=$\frac{3}{4}$×$\frac{1}{2}$×$\frac{1}{3}$=$\frac{1}{8}$.
故ξ分布列为
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{1}{12}$ | $\frac{3}{8}$ | $\frac{5}{12}$ | $\frac{1}{8}$ |
点评 本题考查了相互独立与互斥事件的概率计算公式、随机变量的分布列与数学期望计算公式,考查了推理能力与计算能力,属于中档题.

| A. | [-2,4) | B. | (-1,3] | C. | [-2,-1] | D. | [-1,3] |
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
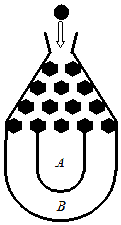 将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落的过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$.
将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落的过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$.