题目内容
直线2x-y+3=0与椭圆
+
=1(a>b>0)的一个焦点和一个顶点的连线垂直,则该椭圆的离心率为 .
| x2 |
| a2 |
| y2 |
| b2 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由题意得:KAB=-
=-
,从而b=
,由a2=b2+c2得:
的比值,进而求出e=
的值.
| 1 |
| 2 |
| b |
| c |
| c |
| 2 |
| c2 |
| a2 |
| c |
| a |
解答:
解:画出草图,如图示:
 ,
,
由题意得:kAB=-
=-
,
∴b=
,由a2=b2+c2得:
=
,
∴e=
=
,
故答案为:
.
 ,
,由题意得:kAB=-
| 1 |
| 2 |
| b |
| c |
∴b=
| c |
| 2 |
| c2 |
| a2 |
| 4 |
| 5 |
∴e=
| c |
| a |
| 2 |
| 5 |
| 5 |
故答案为:
| 2 |
| 5 |
| 5 |
点评:本题考查了椭圆的简单性质,考查直线的斜率问题,是一道基础题.

练习册系列答案
相关题目
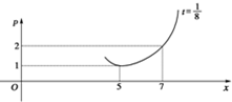 我国加入WTO时,根据达成的协议,若干年内某产品市场供应量p与关税的关系近似满足p(x)=2(1-kt)(x-b)2(其中t为关税的税率,且t∈[0,
我国加入WTO时,根据达成的协议,若干年内某产品市场供应量p与关税的关系近似满足p(x)=2(1-kt)(x-b)2(其中t为关税的税率,且t∈[0,