题目内容
已知函数f（x）=kax-a-x（a＞0且a≠1）在R上是奇函数，且是增函数，则函数g（x）=loga（x-k）的大致图象是（ ）
A、 |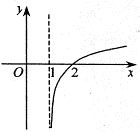
B、 |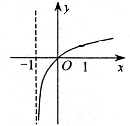
C、 |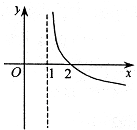
D、 |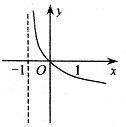
考点：函数的图象,奇偶性与单调性的综合
专题：数形结合,函数的性质及应用
分析：本题考查的知识点是奇偶性的应用，求出k=1，关键单调性求出a的范围，利用对数函数y=logax左右平移即可
解答：
解：因为f（x）=kax-a-x为奇函数，所以f（-x）=-f（x），
即ka-x-ax=-（kax-a-x），得（k-1）（a-x+ax）=0
所以k=1，
又f（x）=ax-a-x是增函数，所以a＞1
将y=logax向右平移一个的单位即得g（x）=loga（x-1）的图象
故选：A
即ka-x-ax=-（kax-a-x），得（k-1）（a-x+ax）=0
所以k=1，
又f（x）=ax-a-x是增函数，所以a＞1
将y=logax向右平移一个的单位即得g（x）=loga（x-1）的图象
故选：A
点评：本题主要考查函数图象的识别和判断，要求熟练掌握函数奇偶性的性质，以及对数函数的图象和性质．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
若函数f（x）=x2+（a-2）x+6在区间[1，+∞）上是增函数，那么实数a的取值范围是（ ）
| A、a≥0 | B、a≤0 |
| C、a≥4 | D、a≤4 |
下列命题中正确的个数是（ ）
（1）若
为单位向量，且
∥
，|
|=1，则
=
；
（2）若|
|=0，则
=0
（3）若
∥
，则|
|=|
|；
（4）若k
=
，则必有k=0（k∈R）；
（5）若k∈R，则k•
=0．
（1）若
| a |
| b |
| a |
| b |
| a |
| b |
（2）若|
| a |
| a |
（3）若
| b |
| a |
| b |
| a |
（4）若k
| a |
| 0 |
（5）若k∈R，则k•
| 0 |
| A、0 | B、1 | C、2 | D、3 |
i是虚数单位，复数z=
=（ ）
| 2-i |
| 1-i |
A、
| ||||
B、
| ||||
| C、1+3i | ||||
| D、3-i |
设等差数列{an}的前n项和为Sn，已知（a5-1）3+2009（a5-1）=1，（a2005-1）3+2009（a2005-1）=-1，则下列结论中正确的是（ ）
| A、S2009=2009，a2005＜a5 |
| B、S2009=2009，a2005＞a5 |
| C、S2009=-2009，a2005≤a5 |
| D、S2009=-2009，a2005≥a5 |