题目内容
已知中心在原点,焦点在坐标轴上的双曲线C经过A(-7,5)、B(-1,-1)两点.
(1)求双曲线C的方程;
(2)设直线l:y=x+m交双曲线C于M、N两点,且线段MN被圆E:x2+y2-12x+n=0(n∈R)三等分,求实数m、n的值.
(1)求双曲线C的方程;
(2)设直线l:y=x+m交双曲线C于M、N两点,且线段MN被圆E:x2+y2-12x+n=0(n∈R)三等分,求实数m、n的值.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)设双曲线C的方程是λx2+μy2=1,代入A(-7,5)、B(-1,-1)两点,即可求双曲线C的方程;
(2)将l:y=x+m代入2y2-x2=1,求出MN的中点P的坐标,利用kPE=-1,求出m,求出直线l截圆E所得弦长,可得圆的方程,即可得出结论.
(2)将l:y=x+m代入2y2-x2=1,求出MN的中点P的坐标,利用kPE=-1,求出m,求出直线l截圆E所得弦长,可得圆的方程,即可得出结论.
解答:
解:(1)设双曲线C的方程是λx2+μy2=1,依题意有
…(2分)
解得λ=-1,μ=2…(3分)
所以所求双曲线的方程是2y2-x2=1…(4分)
(2)将l:y=x+m代入2y2-x2=1,得x2+4mx+(2m2-1)=0…(*)
∴△=(4m)2-4(2m2-1)=8m2+4>0…(6分)
设M(x1,y1),N(x2,y2),MN的中点P(x0,y0),则x1+x2=-4m,x1x2=2m2-1…(7分)
则x0=
=-2m,y0=x0+m=-m,
∴P(-2m,-m)…(8分)
又圆心E(6,0),依题意kPE=-1,故
=-1,即m=-2…(9分)
将m=-2代入(*)得x2-8x+7=0,解得x1=1,x2=7,
∴|MN|=
|x1-x2|=6
…(10分)
故直线l截圆E所得弦长为
|MN|=2
,
又E(6,0)到直线l的距离d=2
…(11分)
∴圆E的半径R=
=
∴圆E的方程是(x-6)2+y2=10…(12分)
∴m=-2,n=26…(13分)
|
解得λ=-1,μ=2…(3分)
所以所求双曲线的方程是2y2-x2=1…(4分)
(2)将l:y=x+m代入2y2-x2=1,得x2+4mx+(2m2-1)=0…(*)
∴△=(4m)2-4(2m2-1)=8m2+4>0…(6分)
设M(x1,y1),N(x2,y2),MN的中点P(x0,y0),则x1+x2=-4m,x1x2=2m2-1…(7分)
则x0=
| x1+x2 |
| 2 |
∴P(-2m,-m)…(8分)
又圆心E(6,0),依题意kPE=-1,故
| m |
| 6+2m |
将m=-2代入(*)得x2-8x+7=0,解得x1=1,x2=7,
∴|MN|=
| 1+12 |
| 2 |
故直线l截圆E所得弦长为
| 1 |
| 3 |
| 2 |
又E(6,0)到直线l的距离d=2
| 2 |
∴圆E的半径R=
(2
|
| 10 |
∴圆E的方程是(x-6)2+y2=10…(12分)
∴m=-2,n=26…(13分)
点评:本题考查双曲线方程,考查直线与双曲线的位置关系,考查圆的方程,考查学生分析解决问题的能力,正确求出双曲线方程是关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
某程序框图如图所示,该程序运行后输出的k的值是( )

| A、4 | B、5 | C、6 | D、7 |
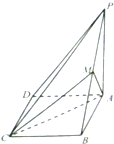 如图,在四棱锥P-ABCD中,ABCD为平行四边形,BC⊥平面PAB,AB=BC=
如图,在四棱锥P-ABCD中,ABCD为平行四边形,BC⊥平面PAB,AB=BC=