题目内容
已知集合M={x||x-1|≥2},N={x|x2-4x≥0},则M∩N( )
| A、{x|x≤0或x≥3} |
| B、{x|x≤0或x≥4} |
| C、{x|x≤-1或x≥3} |
| D、{x|x≤-1或x≥4} |
考点:绝对值不等式的解法
专题:集合
分析:首先化简两个集合,然后进行集合交集的运算.
解答:
解:由已知,M={x||x-1|≥2}={x|x≥3或x≤-1},N={x|x2-4x≥0}={x|x≥4,或x≤0},
∴M∩N={x|≤-1或x≥4}
∴M∩N={x|≤-1或x≥4}
点评:本题考查了集合的化简与运算,集合进行交集运算时,要结合数轴解答.

练习册系列答案
相关题目
若sinθ+cosθ=
,则sinθcosθ的值为( )
| 2 |
| A、-1 | ||
B、-
| ||
C、
| ||
| D、1 |
下列说法不正确的是( )
| A、根据通项公式可以求出数列的任何一项 |
| B、任何数列都有通项公式 |
| C、一个数列可能有几个不同形式的通项公式 |
| D、有些数列可能不存在最大项 |
不等式|4-x|≥1的解集为( )
| A、{x|3≤x≤5} |
| B、{x|x≤3或x≥5} |
| C、{x|-4≤x≤4} |
| D、R |
设|
|=|
|=|
+
|,则
-
与
的夹角为( )
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| A、150° | B、120° |
| C、60° | D、30° |
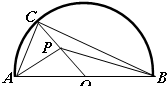 如图,半圆的直径AB=6,O为圆心,C为半圆上不同于A、B的任意一点,若P为半径OC上的动点,则(
如图,半圆的直径AB=6,O为圆心,C为半圆上不同于A、B的任意一点,若P为半径OC上的动点,则(| PA |
| PB |
| PC |
A、-
| ||
B、
| ||
| C、2 | ||
| D、-2 |