题目内容
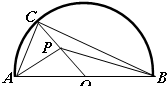如图，半圆的直径AB=6，O为圆心，C为半圆上不同于A、B的任意一点，若P为半径OC上的动点，则（| PA |
| PB |
| PC |
A、-
| ||
B、
| ||
| C、2 | ||
| D、-2 |
考点：向量加减混合运算及其几何意义
专题：平面向量及应用
分析：O为线段AB的中点，利用向量的平行四边形法则可得：
+
=2
．又|
|+|
|=6，利用数量积运算性质、基本不等式可得（
+
）•
=2
•
=-2|
||
|≥-2×(
)2，即可得出．
| PA |
| PB |
| PO |
| PC |
| PO |
| PA |
| PB |
| PC |
| PO |
| PC |
| PO |
| PC |
|
| ||||
| 2 |
解答：
解：∵O为线段AB的中点，∴
+
=2
．
又|
|+|
|=3，
∴（
+
）•
=2
•
=-2|
||
|≥-2×(
)2=-
，
当且仅当|
|=|
|=3时取等号．
故选：A．
| PA |
| PB |
| PO |
又|
| PC |
| PO |
∴（
| PA |
| PB |
| PC |
| PO |
| PC |
| PO |
| PC |
|
| ||||
| 2 |
| 9 |
| 2 |
当且仅当|
| PO |
| PC |
故选：A．
点评：本题考查了向量的平行四边形法则、数量积运算性质、基本不等式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
已知集合M={x||x-1|≥2}，N={x|x2-4x≥0}，则M∩N（ ）
| A、{x|x≤0或x≥3} |
| B、{x|x≤0或x≥4} |
| C、{x|x≤-1或x≥3} |
| D、{x|x≤-1或x≥4} |
函数f（x）的导函数为f′（x），对?x∈R，都有f′（x）＞f（x）成立，若f（ln2）=2，则不等式f（x）＞ex的解是（ ）
| A、x＞1 |
| B、0＜x＜1 |
| C、x＞ln2 |
| D、0＜x＜ln2 |
设等差数列{an}的前n项和为Sn，已知（a2012-1）3+2014a2012=0，a33-3a32+2017a3=4029，则下列结论正确的是（ ）
| A、S2014=2014，a2012＜a3 |
| B、S2014=2014，a2012＞a3 |
| C、S2014=2013，a2012＜a3 |
| D、S2014=2013，a2012＞a3 |