题目内容
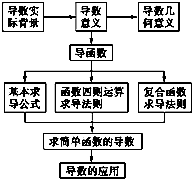
阅读如图所示的知识结构图，“求简单函数的导数”的“上位”要素有 个．
考点：结构图
专题：算法和程序框图
分析：首先对所画结构的每一部分有一个深刻的理解，从头到尾抓住主要脉络进行分解．然后将每一部分进行归纳与提炼，形成一个个知识点并逐一写在矩形框内，最后按其内在的逻辑顺序将它们排列起来并用线段相连，“求简单函数的导数”是建立在熟练掌握“基本求导公式”，“函数四则运算求导法则”和“复合函数求导法则”基础上的，故三者均为其上位．
解答：
解：“求简单函数的导数”是建立在熟练掌握“基本求导公式”，“函数四则运算求导法则”和“复合函数求导法则”基础上的，
故“基本求导公式”，“函数四则运算求导法则”和“复合函数求导法则”均为“求简单函数的导数”的“上位”要素，
故答案为：3
故“基本求导公式”，“函数四则运算求导法则”和“复合函数求导法则”均为“求简单函数的导数”的“上位”要素，
故答案为：3
点评：本题主要考查了结构图，解题的关键弄清综合法属于直接证明，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
已知定义在R上的奇函数f（x）和偶函数g（x）满足f（x）+g（x）=ax-a-x+2（a＞0，且a≠1），若g（2014）=a，则f（-2015）=（ ）
| A、2 |
| B、2-2015-22015 |
| C、22015-22015 |
| D、a2 |
已知集合M={x||x-1|≥2}，N={x|x2-4x≥0}，则M∩N（ ）
| A、{x|x≤0或x≥3} |
| B、{x|x≤0或x≥4} |
| C、{x|x≤-1或x≥3} |
| D、{x|x≤-1或x≥4} |
若f（x）=（m2-1）x2+（m-1）x+（n+2）为奇函数，则m，n的值为（ ）
| A、m=1，n=2 |
| B、m=-1，n=2 |
| C、m=±1，n=-2 |
| D、m=±1，n∈R |
一条直线的倾斜角的正弦值为
，则此直线的斜率是（ ）
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、±
|
设等差数列{an}的前n项和为Sn，已知（a2012-1）3+2014a2012=0，a33-3a32+2017a3=4029，则下列结论正确的是（ ）
| A、S2014=2014，a2012＜a3 |
| B、S2014=2014，a2012＞a3 |
| C、S2014=2013，a2012＜a3 |
| D、S2014=2013，a2012＞a3 |