题目内容
10.设函数f′(x)是函数f(x)(x∈R)的导函数,f(0)=1,且3f(x)=f′(x)-3,则4f(x)>f′(x)( )| A. | ($\frac{ln4}{3}$,+∞) | B. | ($\frac{ln2}{3}$,+∞) | C. | ($\frac{\sqrt{3}}{2}$,+∞) | D. | ($\frac{\sqrt{e}}{3}$,+∞) |
分析 容易求出f′(0)=6,结合条件便可得出函数f(x)的解析式,进而求出导函数,代入4f(x)>f′(x),根据对数函数的单调性及对数的运算便可解出原方程.
解答 解:根据条件,3f(0)=3=f′(0)-3;
∴f′(0)=6;
∴f(x)=2e3x-1,f′(x)=6e3x;
∴由4f(x)>f′(x)得:4(2e3x-1)>6e3x;
整理得,e3x>2;
∴3x>ln2;
∴x>$\frac{ln2}{3}$;
∴原不等式的解集为($\frac{ln2}{3}$,+∞)
故选:B.
点评 本题考查导函数的概念,基本初等函数和复合函数的求导,对数的运算及对数函数的单调性,属于中档题

练习册系列答案
相关题目
19.已知函数f(x)=cosωx+$\sqrt{3}$cosωx(ω>0),如果存在实数x0,使得对任意的实数x,都有f(x0)≤f(x)≤f(x0+2016π)成立,则ω的最小值为( )
| A. | $\frac{1}{4032π}$ | B. | $\frac{1}{2016π}$ | C. | $\frac{1}{4032}$ | D. | $\frac{1}{2016}$ |
2.某几何体的三视图如图所示,其则该几何体的体积是( )
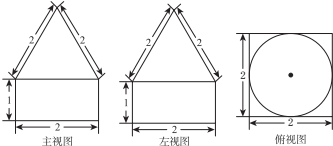

| A. | $2+\frac{{\sqrt{3}}}{3}π$ | B. | $4+\sqrt{3}π$ | C. | $\frac{4}{3}+\frac{{\sqrt{3}}}{3}π$ | D. | $4+\frac{{\sqrt{3}}}{3}π$ |
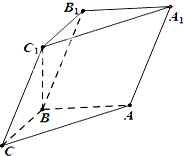 如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=$\frac{π}{3}$.
如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=$\frac{π}{3}$.