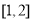题目内容
2.某几何体的三视图如图所示,其则该几何体的体积是( )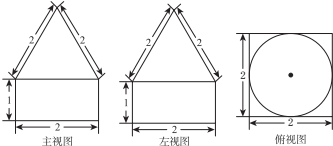
| A. | $2+\frac{{\sqrt{3}}}{3}π$ | B. | $4+\sqrt{3}π$ | C. | $\frac{4}{3}+\frac{{\sqrt{3}}}{3}π$ | D. | $4+\frac{{\sqrt{3}}}{3}π$ |
分析 由三视图可知该几何体由长方体和圆锥构成,利用体积计算公式即可得出.
解答 解:由三视图可知该几何体由长方体和圆锥构成,
∴体积V=2×2×1+$\frac{1}{3}×π×{1}^{2}×\sqrt{3}$=4+$\frac{\sqrt{3}}{3}π$.
故选:D.
点评 本题考查了长方体与圆锥的三视图与体积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
10.设函数f′(x)是函数f(x)(x∈R)的导函数,f(0)=1,且3f(x)=f′(x)-3,则4f(x)>f′(x)( )
| A. | ($\frac{ln4}{3}$,+∞) | B. | ($\frac{ln2}{3}$,+∞) | C. | ($\frac{\sqrt{3}}{2}$,+∞) | D. | ($\frac{\sqrt{e}}{3}$,+∞) |
14.已知函数f(x)=$\left\{{\begin{array}{l}{{2^x}-\frac{a}{3},x≤0}\\{lnx-2x+a,x>0}\end{array}}$有三个不同的零点,则实数a的取值范围是( )
| A. | (1+ln2,3] | B. | (ln2,3] | C. | (0,1+ln2) | D. | (0,3] |
11.已知A(0,1)和直线l:x=-5,抛物线y2=4x上动点P到l的距离为d,则|PA|+d的最小值是( )
| A. | 6 | B. | $5+\sqrt{2}$ | C. | $4+\sqrt{2}$ | D. | $4\sqrt{2}$ |
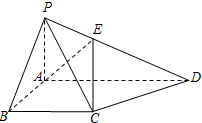 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,∠ABC=∠BAD=90°,且PA=AB=BC=$\frac{1}{2}$AD=1,PA⊥平面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,∠ABC=∠BAD=90°,且PA=AB=BC=$\frac{1}{2}$AD=1,PA⊥平面ABCD. ,
,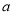 是
是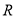 上的常数,若
上的常数,若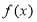 的值域为
的值域为 ,则
,则 取值范围为( )
取值范围为( )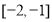 B.
B.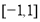
 D.
D.