题目内容
20.设y3+3x2y+x=1确定y是x的函数,求y′及y′|x=0.分析 两边对x求导,可得y′,求出x=0,y=1,计算即可得到y′|x=0.
解答 解:y3+3x2y+x=1,
两边对x求导,可得,
3y2y′+6yx+1=0,
即为y′=$\frac{-1-6xy}{3{y}^{2}}$,
x=0时,y=1,
则y′|x=0=$\frac{-1-6×0×1}{3×1}$=-$\frac{1}{3}$.
点评 本题考查导数的运算,注意运用两边对x求导,考查运算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.设函数f′(x)是函数f(x)(x∈R)的导函数,f(0)=1,且3f(x)=f′(x)-3,则4f(x)>f′(x)( )
| A. | ($\frac{ln4}{3}$,+∞) | B. | ($\frac{ln2}{3}$,+∞) | C. | ($\frac{\sqrt{3}}{2}$,+∞) | D. | ($\frac{\sqrt{e}}{3}$,+∞) |
11.已知A(0,1)和直线l:x=-5,抛物线y2=4x上动点P到l的距离为d,则|PA|+d的最小值是( )
| A. | 6 | B. | $5+\sqrt{2}$ | C. | $4+\sqrt{2}$ | D. | $4\sqrt{2}$ |
 ,
,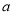 是
是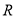 上的常数,若
上的常数,若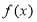 的值域为
的值域为 ,则
,则 取值范围为( )
取值范围为( )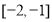 B.
B.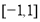
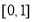 D.
D.