题目内容
3.已知三棱锥A-BCD中,平面ABD⊥平面BCD,BC⊥CD,BC=CD=4,AB=AD=$2\sqrt{3}$,则三棱锥A-BCD的外接球的大圆面积为9π.分析 利用已知三棱锥A-BCD的特点AB=AC=AD,先确定△ABD的外心O,及外接圆的半径,然后证明O也是三棱锥A-BCD的外接球的球心,即可解答.
解答 解:∵如图取BD的中点E,连接AE,CE.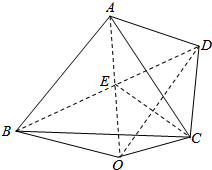
则AE⊥BD,CE⊥BD.
∵平面ABD⊥平面BCD,
平面ABD∩平面BCD=BD,
∴AE⊥平面BCD,
又∵CE?平面BCD,
∴AE⊥CE.
设△ABD的外接圆的圆心为O,半径为r.
∵AB=AD,
∴圆心O在AE所在的直线上.
∴r2=BE2+OE2=BE2+(r-AE)2.
∵在Rt△BCD中,BD=$\sqrt{16+16}$=4$\sqrt{2}$.
∴BE=EC=2$\sqrt{2}$.
∴在Rt△ABE中,AE=$\sqrt{12-8}$=2.
∴r2=8+(r-2)2,解得r=3.
∴OE=1.
在Rt△OEC中,OC=$\sqrt{O{E}^{2}+E{C}^{2}}$=3.
∴OA=OB=OC=OD=3.
∴点O是三棱锥A-BCD的外接球的球心,则球半径R=3.
∴大圆面积S=πR2=9π.
故答案为:9π.
点评 本题考查球内接多面体及其度量,考查空间想象能力,计算能力,解答的关键是确定球心位置,利用已知三棱锥的特点是解决问题关键,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.哈六中数学组推出微信订阅号(公众号hl15645101785)后,受到家长和学生们的关注,为了更好的为学生和家长提供帮助,我们在某时间段在线调查了60位更关注栏目1或栏目2(2选一)的群体身份样本得到如下列联表,已知在样本中关注栏目1与关注栏目2的人数比为2:1,在关注栏目1中的家长与学生人数比为5:3,在关注栏目2中的家长与学生人数比为1:3
(1)完成列联表,并根据列联表的数据,若按99%的可靠性要求,能否认为“更关注栏目1或栏目2与群体身份有关系”;
(2)如果把样本频率视为概率,随机回访两位关注者,更关注栏目1的人数记为随机变量X,求X的分布列和期望;
(3)由调查样本对两个栏目的关注度,请你为数学组教师提供建议应该更侧重充实哪个栏目的内容,并简要说明理由.
(${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.)
| 栏目1 | 栏目2 | 合计 | |
| 家长 | |||
| 学生 | |||
| 合计 |
(2)如果把样本频率视为概率,随机回访两位关注者,更关注栏目1的人数记为随机变量X,求X的分布列和期望;
(3)由调查样本对两个栏目的关注度,请你为数学组教师提供建议应该更侧重充实哪个栏目的内容,并简要说明理由.
| P(K2≥x0) | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| x0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
10.设函数f′(x)是函数f(x)(x∈R)的导函数,f(0)=1,且3f(x)=f′(x)-3,则4f(x)>f′(x)( )
| A. | ($\frac{ln4}{3}$,+∞) | B. | ($\frac{ln2}{3}$,+∞) | C. | ($\frac{\sqrt{3}}{2}$,+∞) | D. | ($\frac{\sqrt{e}}{3}$,+∞) |
11.已知A(0,1)和直线l:x=-5,抛物线y2=4x上动点P到l的距离为d,则|PA|+d的最小值是( )
| A. | 6 | B. | $5+\sqrt{2}$ | C. | $4+\sqrt{2}$ | D. | $4\sqrt{2}$ |

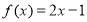 ,
, ,则
,则 的解析式是_______.
的解析式是_______.