题目内容
6.已知函数f(x)=$\frac{1}{3}{x^3}$-$\frac{3}{2}{x^2}$+2x+3a+b恰有3个不同的零点,则f(0)的取值范围是(-$\frac{5}{6}$,-$\frac{2}{3}$).分析 求函数的导数,求出函数的极大值和极小值,利用函数f(x)恰有3个不同的零点,转化为f(x)极大>0且f(x)极小<0,求出a,b的关系即可得到结论.
解答 解:函数的导数为f′(x)=x2-3x+2=(x-1)(x-2),
由f′(x)>0得x>2或x<1,此时函数单调递增,
由f′(x)<0,得1<x<2,此时函数单调递减,
即当x=1时,函数取得极大值,f(1)=$\frac{1}{3}-\frac{3}{2}$+2+3a+b=$\frac{5}{6}$+3a+b,
即当x=2时,函数取得极小值,f(2)=$\frac{8}{3}-$6+4+3a+b=$\frac{2}{3}$+3a+b,
若函数f(x)=$\frac{1}{3}{x^3}$-$\frac{3}{2}{x^2}$+2x+3a+b恰有3个不同的零点,
则f(x)极大>0且f(x)极小<0,
即f(x)极大=$\frac{5}{6}$+3a+b>0且f(x)极小=$\frac{2}{3}$+3a+b<0,
则-$\frac{5}{6}$<3a+b<-$\frac{2}{3}$,
则f(0)=3a+b,
即f(0)的取值范围是(-$\frac{5}{6}$,-$\frac{2}{3}$),
故答案为:(-$\frac{5}{6}$,-$\frac{2}{3}$)
点评 本题主要考查函数零点的应用,求函数的导数,利用函数极值和函数的导数的关系是解决本题的关键.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
10.设函数f′(x)是函数f(x)(x∈R)的导函数,f(0)=1,且3f(x)=f′(x)-3,则4f(x)>f′(x)( )
| A. | ($\frac{ln4}{3}$,+∞) | B. | ($\frac{ln2}{3}$,+∞) | C. | ($\frac{\sqrt{3}}{2}$,+∞) | D. | ($\frac{\sqrt{e}}{3}$,+∞) |
14.已知函数f(x)=$\left\{{\begin{array}{l}{{2^x}-\frac{a}{3},x≤0}\\{lnx-2x+a,x>0}\end{array}}$有三个不同的零点,则实数a的取值范围是( )
| A. | (1+ln2,3] | B. | (ln2,3] | C. | (0,1+ln2) | D. | (0,3] |
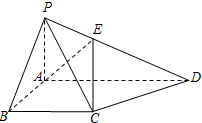 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,∠ABC=∠BAD=90°,且PA=AB=BC=$\frac{1}{2}$AD=1,PA⊥平面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,∠ABC=∠BAD=90°,且PA=AB=BC=$\frac{1}{2}$AD=1,PA⊥平面ABCD.