题目内容
18.若-1<x<4是x>2m2-3的充分不必要条件,则实数m的取值范围是( )| A. | [-3,3] | B. | (-∞,-3]∪[3,+∞) | C. | (-∞,-1]∪[1,+∞) | D. | [-1,1] |
分析 -1<x<4是x>2m2-3的充分不必要条件,可得-1≥2m2-3,解得m范围.
解答 解:-1<x<4是x>2m2-3的充分不必要条件,
∴-1≥2m2-3,解得-1≤m≤1.
故选:D.
点评 本题考查了不等式的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
8.数列{an}的通项公式an=ncos$\frac{nπ}{2}$,其前n项和为Sn,则S2013等于( )
| A. | 1006 | B. | 2012 | C. | 503 | D. | 0 |
6.已知数列{an}中,a1=1,前n项和为Sn,且点P(an,an+1)在直线y=x+1上,则$\frac{1}{S_1}+\frac{1}{S_2}+\frac{1}{S_3}+…+\frac{1}{S_n}$=( )
| A. | $\frac{2n}{n+1}$ | B. | $\frac{2}{n(n+1)}$ | C. | $\frac{n(n+1)}{2}$ | D. | $\frac{n}{2(n+1)}$ |
13.如果z 1、z 2∈C且z 1$\overline{{z}_{2}}$=$\overline{{z}_{1}}$z 2≠0,则 $\frac{{z}_{1}}{{z}_{2}}$是( )
| A. | 虚数 | B. | 纯虚数 | C. | 实数 | D. | 不确定 |
3.某校高三共有三个班,其各班人数如表:
(1)从三个班中选一名学生会主席,有多少种不同的选法?
(2)从(1)班、(2)班男生中或从(3)班女生中选一名学生任学生会生活部部长,有多少种不同的选法?
| 班级 | 男生数 | 女生数 | 总数 |
| 高三(1) | 30 | 20 | 50 |
| 高三(2) | 30 | 30 | 60 |
| 高三(3) | 35 | 20 | 55 |
(2)从(1)班、(2)班男生中或从(3)班女生中选一名学生任学生会生活部部长,有多少种不同的选法?
10.复数(i-$\frac{1}{i}$)3的虚部是( )
| A. | -8 | B. | -8i | C. | 8 | D. | 8i |
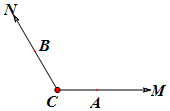 已知点A,B分别在射线CM,CN(不含端点C)上运动,$∠MCN=\frac{2π}{3}$,在△ABC中,角A,B,C所对的边分别是a,b,c.
已知点A,B分别在射线CM,CN(不含端点C)上运动,$∠MCN=\frac{2π}{3}$,在△ABC中,角A,B,C所对的边分别是a,b,c.