题目内容
在△ABC中，AB=3，AC=2，BC=
，则
•
=（ ）
| 10 |
| CA |
| AB |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
考点：平面向量数量积的运算
专题：平面向量及应用
分析：根据余弦定理求出cosA，然后根据向量的数量积的公式即可得到结论．
解答：
解：∵AB=3，AC=2，BC=
，
∴cosA=
=
=
=
，
则
•
=|
|•|
|cos（π-A）=-|
|•|
|cosA=-2×3×
=-
，
故选：D．
| 10 |
∴cosA=
| AC2+AB2-BC2 |
| 2AC•AB |
| 22+32-10 |
| 2×2×3 |
| 3 |
| 12 |
| 1 |
| 4 |
则
| CA |
| AB |
| CA |
| AB |
| CA |
| AB |
| 1 |
| 4 |
| 3 |
| 2 |
故选：D．
点评：本题主要考查数量积的计算，根据余弦定理求出cosB是解决本题的关键，要求熟练掌握相应的公式．
练习册系列答案
相关题目
不等式|1-x|≥2的解集为（ ）
| A、{x|x≤-1或x≥3} |
| B、{x|x≥3} |
| C、{x|-1≤x≤3} |
| D、R |
若sin2x•sin3x=cos2x•cos3x，则x的一个值为（ ）
| A、36° | B、45° |
| C、18° | D、30° |
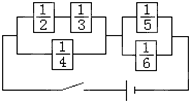在如图所示的电路中，5只箱子表示保险匣，箱中所示数值表示通电时保险丝被切断的概率，若各保险匣之间互不影响，则当开关合上时，电路畅通的概率是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
已知无穷等差数列{a n}，前n项和Sn中，S6＜S7，且S7＞S8，则（ ）
| A、在数列{an }中a7 最大 |
| B、在数列{an}中，a3或a4最大 |
| C、前三项之和S3必与前11项之和S11相等 |
| D、当n≥8时，an＜0． |
已知函数f（x）的定义域为R，其导函数为f′（x），且f（x）+xf′（x）＜0恒成立，则三个数-f（-1），f（1），3f（3）的大小关系为（ ）
| A、-f（-1）＜f（1）＜3f（3） |
| B、f（1）＜-f（-1）＜3f（3） |
| C、-f（-1）＜3f（3）＜f（1） |
| D、3f（3）＜f（1）＜-f（-1） |
已知扇形的圆心角为
弧度，半径为2，则扇形的面积为（ ）
| 2π |
| 3 |
A、
| ||
B、
| ||
| C、2π | ||
D、
|