Question

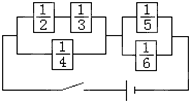在如图所示的电路中，5只箱子表示保险匣，箱中所示数值表示通电时保险丝被切断的概率，若各保险匣之间互不影响，则当开关合上时，电路畅通的概率是（　　）

• A、

  551

  720

• B、

  29

  144

• C、

  29

  72

• D、

  29

  36

Answer 1

考点：n次独立重复试验中恰好发生k次的概率

专题：概率与统计

分析：前两个盒子为串联线路，求出它们不畅通的概率，利用对立事件的概率求出前3个畅通的概率，后2个盒子为并联线路，求出它们不畅通的概率，前3个盒子和后2个盒子又是串联线路，利用独立事件同时发生的概率公式，即可求电路畅通的概率．

解答： 解：前两个盒子畅通的畅通的概率为

1

2

×

2

3

=

1

3

，所以不畅通的概率为1-

1

3

=

2

3

．
则前三个盒子畅通的概率为1-

2

3

×

1

4

=

5

6

 
后两个盒子畅通的概率为1-

1

5

×

5

6

=

29

30

．
所以当开关合上时，电路畅通的概率是

29

30

×

5

6

=

29

36

，
故选：D．

点评：本题主要考查相互独立事件的概率公式，考查学生分析问题的能力．综合性较强，属于中档题．