题目内容
5.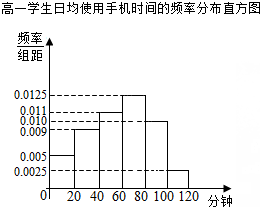 某学校为了了解学生使用手机的情况,分别在高一和高二两个年级各随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生日均使用手机时间的频率分布直方图和频数分布表,将使用手机时间不低于80分钟的学生称为“手机迷”.
某学校为了了解学生使用手机的情况,分别在高一和高二两个年级各随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生日均使用手机时间的频率分布直方图和频数分布表,将使用手机时间不低于80分钟的学生称为“手机迷”.高二学生日均使用手机时间的频数分布表
| 时间分组 | 频数 |
| [0,20) | 12 |
| [20,40) | 20 |
| [40,60) | 24 |
| [60,80) | 26 |
| [80,100) | 14 |
| [100,120] | 4 |
(Ⅱ)在高一的抽查中,已知随机抽到的女生共有55名,其中10名为“手机迷”.根据已知条件完成下面的2×2列联表,并据此资料你有多大的把握认为“手机迷”与性别有关?
| 非手机迷 | 手机迷 | 合计 | |
| 男 | 30 | 15 | 45 |
| 女 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
| 参考数据 | P(k2≥x0) | 0.15 | 0.10 | 0.05 | 0.025 |
| x0 | 2.072 | 2.706 | 3.841 | 5.024 |
分析 (Ⅰ)将频率视为概率,即可得出结论.
(Ⅱ)利用频率分布直方图直接完成2×2列联表,通过计算K2,说明有90%的把握认为“手机迷”与性别有关.
解答 解:(Ⅰ)由频率分布直方图可知,高一学生是“手机迷”的概率为P1=(0.0025+0.010)×20=0.25(2分)
由频数分布表可知,高二学生是“手机迷”的概率为${P_2}=\frac{14+4}{100}=0.18$(4分)
因为P1>P2,所以高一年级的学生是“手机迷”的概率大.(5分)
(Ⅱ)由频率分布直方图可知,在抽取的100人中,
“手机迷”有(0.010+0.0025)×20×100=25(人),
非手机迷有100-25=75(人).(6分)
从而2×2列联表如下:
| 非手机迷 | 手机迷 | 合计 | |
| 男 | 30 | 15 | 45 |
| 女 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
将2×2列联表中的数据代入公式计算,得${k^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}=\frac{{100×{{(30×10-45×15)}^2}}}{75×25×45×55}=\frac{100}{33}≈3.030$(11分)
因为3.030>2.706,所以有90%的把握认为“手机迷”与性别有关.(12分)
点评 本题考查独立性检验以及概率的计算,考查基本知识的应用,属于中档题.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
13.一个口袋内装有大小相同的5只球,其中3只白球,2只黑球,从中一次摸出两个球,则摸出的两个都是白球的概率是( )
| A. | $\frac{2}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{1}{5}$ | D. | $\frac{7}{10}$ |
20.已知函数f(x)=-lnx+x+h,在区间$[{\frac{1}{e},e}]$上任取三个实数a,b,c均存在以f(a),f(b),f(c)为边长的三角形,则实数h的取值范围是( )
| A. | (-∞,-1) | B. | (-∞,e-3) | C. | (-1,+∞) | D. | (e-3,+∞) |
 如图,直线PB与圆O交于A,B两点,OD⊥AB于点D,PC是圆O的切线,切点为C.
如图,直线PB与圆O交于A,B两点,OD⊥AB于点D,PC是圆O的切线,切点为C.