一个口袋内装有大小相同的5只球.其中3只白球.2只黑球.从中一次摸出两个球.则摸出的两个都是白球的概率是( )A．$\frac{2}{5}$B．$\frac{3}{10}$C．$\frac{1}{5}$D．$\frac{7}{10}$ 题目和参考答案——青夏教育精英家教网——

题目内容

13．一个口袋内装有大小相同的5只球，其中3只白球，2只黑球，从中一次摸出两个球，则摸出的两个都是白球的概率是（　　）

A．

$\frac{2}{5}$

B．

$\frac{3}{10}$

C．

$\frac{1}{5}$

D．

$\frac{7}{10}$

分析从中一次摸出两个球，先求出基本事件总数，再求出摸出的两个都是白球，包含的基本事件个数，由此能求出摸出的两个都是白球的概率．

解答解：一个口袋内装有大小相同的5只球，其中3只白球，2只黑球，
从中一次摸出两个球，基本事件总数$n={C}_{5}^{2}$=10，
摸出的两个都是白球，包含的基本事件个数m=${C}_{3}^{2}$=3，
∴摸出的两个都是白球的概率是p=$\frac{m}{n}$=$\frac{3}{10}$．
故选：B．

点评本题考查摸出的两个球都是白球的概率的求法，是基础题，解题时要认真审题，注意等可能事件概率计算公式的合理运用．

练习册系列答案

创新课时作业系列答案

希望英语测试卷系列答案

小学课课通系列答案

一线调研卷系列答案

全能提分系列答案

中考试题专题训练系列答案

通城学典中考总复习系列答案

蓉城学堂阅读周练系列答案

文言文图解注译系列答案

课时配套练系列答案

相关题目

3．已知p：x²-2x-8≤0，q：x²+mx-2m²≤0，m＞0．
（1）若q是p的必要不充分条件，求m的取值范围；
（2）若￢p是￢q的充分不必要条件，求m的取值范围．

4．已知命题p，q，则“￢p为假命题”是“p∧q是真命题”的（　　）

	A．	充分而不必要条件		B．	必要而不充分条件
	C．	充要条件		D．	既不充分也不必要条件

1．若a=3^0.5，b=ln2，c=log₃sin$\frac{π}{6}$，则下列不等式正确的是（　　）

8．在△ABC中，角A，B，C分别为三个内角，B=2A，向量$\overrightarrow{m}$=（cosA，-sinB），向量$\overrightarrow{n}$=（cosB，sinA），且向量$\overrightarrow{m}$⊥$\overrightarrow{n}$．
（1）求角B的大小；
（2）设f（x）=cos（ωx-$\frac{B}{2}$）+sinωx（ω＞0），且f（x）的最小正周期为π，求f（x）的单调递增区间及f（x）在[0，$\frac{π}{2}$]上的最大值．

18．函数f（x）=3+6sin（π+x）-cos2x（x∈R）的最大值和最小值之和是（　　）

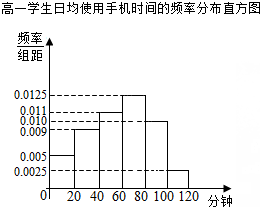某学校为了了解学生使用手机的情况，分别在高一和高二两个年级各随机抽取了100名学生进行调查．下面是根据调查结果绘制的学生日均使用手机时间的频率分布直方图和频数分布表，将使用手机时间不低于80分钟的学生称为“手机迷”．
高二学生日均使用手机时间的频数分布表

时间分组	频数
[0，20）	12
[20，40）	20
[40，60）	24
[60，80）	26
[80，100）	14
[100，120]	4

（Ⅰ）将频率视为概率，估计哪个年级的学生是“手机迷”的概率大？请说明理由．
（Ⅱ）在高一的抽查中，已知随机抽到的女生共有55名，其中10名为“手机迷”．根据已知条件完成下面的2×2列联表，并据此资料你有多大的把握认为“手机迷”与性别有关？

	非手机迷	手机迷	合计
男	30	15	45
女	45	10	55
合计	75	25	100

附：随机变量${k^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$（其中n=a+b+c+d为样本总量）．

参考数据	P（k²≥x₀）	0.15	0.10	0.05	0.025
参考数据	x₀	2.072	2.706	3.841	5.024

2．已知函数f（x）=|x²-1|+x²+ax．
（1）若a=2，求函数f（x）的零点；
（2）求f（x）的单调区间；
（3）若函数f（x）在区间[0，2]上的最大值为9，求实数a的值．

3．已知圆C的方程为x²+y²=16，直线l：x+y-8=0，点P是直线l上的一动点，过P做圆C的两条切线，切点分别为A，B，当四边形PAOB的面积最小时，直线AB的方程为（　　）