题目内容
20.已知函数f(x)=-lnx+x+h,在区间$[{\frac{1}{e},e}]$上任取三个实数a,b,c均存在以f(a),f(b),f(c)为边长的三角形,则实数h的取值范围是( )| A. | (-∞,-1) | B. | (-∞,e-3) | C. | (-1,+∞) | D. | (e-3,+∞) |
分析 由条件可得2f(x)min>f(x)max且f(x)min>0,再利用导数求得函数的最值,从而得出结论.
解答 解:任取三个实数a,b,c均存在以f(a),f(b),f(c)为边长的三角形,
等价于f(a)+f(b)>f(c)恒成立,可转化为2f(x)min>f(x)max且f(x)min>0.
令$f'(x)=-\frac{1}{x}+1=\frac{x-1}{x}=0$得x=1.
当$\frac{1}{e}<x<1$时,f'(x)<0;当1<x<e时,f'(x)>0;
所以当x=1时,f(x)min=f(1)=1+h,$f{(x)_{max}}=max\{f(\frac{1}{e}),f(e)\}$=$max\left\{{\frac{1}{e}+1+h,e-1+h}\right\}$=e-1+h,
从而可得$\left\{\begin{array}{l}2(1+h)>e-1+h\\ h+1>0\end{array}\right.$,解得h>e-3,
故选:D.
点评 本题主要考查利用导数研究函数的单调性,函数的恒成立问题,求函数的最值,属于中档题.

练习册系列答案
相关题目
11.定义域为R的函数f(x)满足f(x+2)=2f(x),当x∈[0,2)时,f(x)=$\left\{\begin{array}{l}{x^2}-x,x∈[0,1)\\-{(\frac{1}{2})^{|{x-\frac{3}{2}}|}},x∈[1,2)\end{array}$,若当x∈[-4,-2)时,不等式f(x)≥$\frac{t^2}{4}-t+\frac{1}{2}$恒成立,则实数t的取值范围是( )
| A. | [2,3] | B. | [1,3] | C. | [1,4] | D. | [2,4] |
15.在等比数列{an}中,已知${a_6}{a_{13}}=\sqrt{2}$,则a6a7a8a9a10a11a12a13=( )
| A. | 4 | B. | $2\sqrt{2}$ | C. | 2 | D. | $\sqrt{2}$ |
5.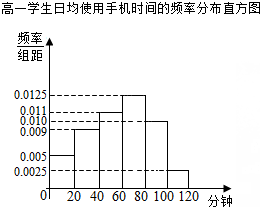 某学校为了了解学生使用手机的情况,分别在高一和高二两个年级各随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生日均使用手机时间的频率分布直方图和频数分布表,将使用手机时间不低于80分钟的学生称为“手机迷”.
某学校为了了解学生使用手机的情况,分别在高一和高二两个年级各随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生日均使用手机时间的频率分布直方图和频数分布表,将使用手机时间不低于80分钟的学生称为“手机迷”.
高二学生日均使用手机时间的频数分布表
(Ⅰ)将频率视为概率,估计哪个年级的学生是“手机迷”的概率大?请说明理由.
(Ⅱ)在高一的抽查中,已知随机抽到的女生共有55名,其中10名为“手机迷”.根据已知条件完成下面的2×2列联表,并据此资料你有多大的把握认为“手机迷”与性别有关?
附:随机变量${k^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$(其中n=a+b+c+d为样本总量).
 某学校为了了解学生使用手机的情况,分别在高一和高二两个年级各随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生日均使用手机时间的频率分布直方图和频数分布表,将使用手机时间不低于80分钟的学生称为“手机迷”.
某学校为了了解学生使用手机的情况,分别在高一和高二两个年级各随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生日均使用手机时间的频率分布直方图和频数分布表,将使用手机时间不低于80分钟的学生称为“手机迷”.高二学生日均使用手机时间的频数分布表
| 时间分组 | 频数 |
| [0,20) | 12 |
| [20,40) | 20 |
| [40,60) | 24 |
| [60,80) | 26 |
| [80,100) | 14 |
| [100,120] | 4 |
(Ⅱ)在高一的抽查中,已知随机抽到的女生共有55名,其中10名为“手机迷”.根据已知条件完成下面的2×2列联表,并据此资料你有多大的把握认为“手机迷”与性别有关?
| 非手机迷 | 手机迷 | 合计 | |
| 男 | 30 | 15 | 45 |
| 女 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
| 参考数据 | P(k2≥x0) | 0.15 | 0.10 | 0.05 | 0.025 |
| x0 | 2.072 | 2.706 | 3.841 | 5.024 |
10.已知i为虚数单位,则z=$\frac{1+2{i}^{3}}{2+i}$的值为( )
| A. | 0 | B. | i | C. | -i | D. | 1+i |