题目内容
16.设数列{an}的前n项和为Sn,且2an=Sn+2.(Ⅰ)求{an}的通项公式;
(Ⅱ)设${b_n}=\frac{n}{a_n}$,求数列的前n项和Tn.
分析 (Ⅰ)求出a1=2.利用Sn-Sn-1,推出关系式,判断数列是等比数列,求出通项公式.
(Ⅱ)由(Ⅰ)求出${b_n}=\frac{n}{2^n}$,利用错位相减法求解数列的和即可.
解答 (本小题满分12分)
解:(Ⅰ)当n=1时,由2a1=S1+2=a1+2,得a1=2.(1分)
当n≥2时,由$\left\{\begin{array}{l}2{a_n}={S_n}+2\\ 2{a_{n-1}}={S_{n-1}}+2\end{array}\right.$(3分)
两式相减并化简得$\frac{a_n}{{{a_{n-1}}}}=2$,(4分)
所以数列{an}是首项为2,公比为2的等比数列,故${a_n}={2^n}$.(6分)
(Ⅱ)由(Ⅰ)知${a_n}={2^n}$,所以${b_n}=\frac{n}{2^n}$,(7分)
所以${T_n}={b_1}+{b_2}+…+{b_n}=\frac{1}{2}+\frac{2}{2^2}+\frac{3}{2^3}+…+\frac{n-1}{{{2^{n-1}}}}+\frac{n}{2^n}$①(8分)
①式两边乘以$\frac{1}{2}$,得$\frac{1}{2}{T_n}=\frac{1}{2^2}+\frac{2}{2^3}+\frac{3}{2^4}+…+\frac{n-1}{2^n}+\frac{n}{{{2^{n+1}}}}$②(9分)
①-②得$\frac{1}{2}{T_n}=\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+…+\frac{1}{2^n}-\frac{n}{{{2^{n+1}}}}$(10分)
=$\frac{{\frac{1}{2}×[{1-{{({\frac{1}{2}})}^n}}]}}{{1-\frac{1}{2}}}-\frac{n}{{{2^{n+1}}}}=1-\frac{1}{2^n}-\frac{n}{{{2^{n+1}}}}$(11分)
所以${T_n}=2-\frac{1}{{{2^{n-1}}}}-\frac{n}{2^n}$.(12分)
点评 本题考查数列的通项公式以及数列求和的方法,考查计算能力.

 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案| A. | y=±$\frac{1}{2}$x | B. | y=±$\frac{\sqrt{2}}{2}$x | C. | y=±$\frac{1}{3}$x | D. | y=±$\frac{\sqrt{3}}{3}$x |
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | [2,3] | B. | [1,3] | C. | [1,4] | D. | [2,4] |
| A. | a>b>c | B. | b>a>c | C. | b>c>a | D. | c>a>b |
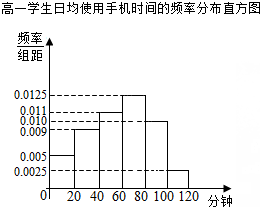 某学校为了了解学生使用手机的情况,分别在高一和高二两个年级各随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生日均使用手机时间的频率分布直方图和频数分布表,将使用手机时间不低于80分钟的学生称为“手机迷”.
某学校为了了解学生使用手机的情况,分别在高一和高二两个年级各随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生日均使用手机时间的频率分布直方图和频数分布表,将使用手机时间不低于80分钟的学生称为“手机迷”.高二学生日均使用手机时间的频数分布表
| 时间分组 | 频数 |
| [0,20) | 12 |
| [20,40) | 20 |
| [40,60) | 24 |
| [60,80) | 26 |
| [80,100) | 14 |
| [100,120] | 4 |
(Ⅱ)在高一的抽查中,已知随机抽到的女生共有55名,其中10名为“手机迷”.根据已知条件完成下面的2×2列联表,并据此资料你有多大的把握认为“手机迷”与性别有关?
| 非手机迷 | 手机迷 | 合计 | |
| 男 | 30 | 15 | 45 |
| 女 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
| 参考数据 | P(k2≥x0) | 0.15 | 0.10 | 0.05 | 0.025 |
| x0 | 2.072 | 2.706 | 3.841 | 5.024 |