Question

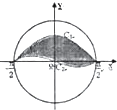如图，在一圆形水域内有一片“枯叶”，它的边界由曲线C₁：f（x）=cosx与曲线C₂：g（x）=

2

π

x-sinx围成，圆的方程为：x²+y²=

π2

4

，假设“枯叶”在水中保持静止，现有一小孩向水中投掷一颗沙粒，则此沙粒恰好砸中“枯叶”的概率为（　　）

• A、

  2

  π2

• B、

  8

  π3

• C、

  8

  π2

• D、

  4

  π3

Answer 1

考点：几何概型

专题：概率与统计

分析：根据几何概型的概率公式，利用积分求出阴影部分的面积即可得到结论．

解答： 解：根据积分的几何意义可知阴影部分的面积S=∫

π 2 - π 2

[f（x）-g（x）]dx
=∫

π 2 - π 2

（cosx-

2

π

x+sinx）dx
=（sinx-

x2

π

-cosx）|

π 2 - π 2

=1-

π

4

-（-1-

π

4

）=2，
圆的面积S=π×(

π

2

)2=

π3

4

，
故沙粒恰好砸中“枯叶”的概率P=

S阴影

S圆

=

2

π3 4

=

8

π3

，
故选：B．

点评：本题主要考查几何概型的概率计算，利用积分的几何意义求出阴影部分的面积是解决本题的关键．