题目内容
若i(i是虚数单位)是关于x的方程x2+px+q=0(p,q∈R)的一个根,则p-q=( )
| A、-1 | B、0 | C、-2 | D、1 |
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:根据复数的根的定义以及复数相等的关系,代入方程即可得到结论.
解答:
解:∵i(i是虚数单位)是关于x的方程x2+px+q=0(p,q∈R)的一个根,
∴i2+pi+q=0,
即q-1+pi=0,
即q-1=0,且p=0,
解得q=1,p=0,
则p-q=0-1=-1,
故选:A.
∴i2+pi+q=0,
即q-1+pi=0,
即q-1=0,且p=0,
解得q=1,p=0,
则p-q=0-1=-1,
故选:A.
点评:本题主要考查复数根的应用,利用复数相等是解决本题的关键,比较基础.

练习册系列答案
相关题目
设随机变量X服从二项分布X~B(5,
),则函数f(x)=x2+4x+X存在零点的概率是( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
(1-2x)4(x+2)3的展开式中x2项的系数是( )
| A、294 | B、96 |
| C、102 | D、198 |
设a=40.6,b=0.63,c=log0.63,则a、b、c的大小关系是( )
| A、a<b<c |
| B、b<a<c |
| C、b<c<a |
| D、c<b<a |
若某空间几何体的三视图如图所示,则该几何体的体积是( )
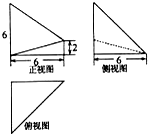

| A、16 | B、32 | C、48 | D、144 |
有4个兴趣小组,甲、乙两位同学各自参加其中一个小组,每位同学参加各个小组的可能性相同,则这两位同学参加同一个兴趣小组的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知定义在R上的函数f(x)=ex+x2-x+sinx,则曲线y=f(x)在点(0,f(0))处的切线方程是( )
| A、y=2x-1 |
| B、y=x+1 |
| C、y=3x-2 |
| D、y=-2x+3 |
某几何体的三视图如图所示,则该几何体的体积为( )


A、4-
| ||
B、4-
| ||
C、6-
| ||
D、8-
|
