题目内容
在平面直角坐标系中,已知An(n,an)、Bn(n,bn)、Cn(n-1,0)(n∈N*),满足向量
与向量
共线,且点Bn(n,bn)(n∈N*)都在斜率为6的同一条直线上.
(1)试用a1,b1与n来表示an;
(2)设a1=a,b1=-a,且12<a≤15,求数{an}中的最小值的项.
| A1An+1 |
| BnCn |
(1)试用a1,b1与n来表示an;
(2)设a1=a,b1=-a,且12<a≤15,求数{an}中的最小值的项.
考点:平面向量数量积的运算
专题:综合题,等差数列与等比数列,平面向量及应用
分析:(1)由点Bn(n,bn)(n∈N*)都在斜率为6的同一条直线上,得
=6,即bn+1-bn=6,由此可求得bn,由向量
与向量
共线,得an+1-an=bn,利用累加法可表示an;
(2)代入a1=a,b1=-a,得an=a-a(n-1)+3(n-1)(n-2)=3n2-(9+a)n+6+2a.根据二次函数的性质及对称轴范围可求得结果;
| bn+1-bn |
| (n+1)-n |
| A1An+1 |
| BnCn |
(2)代入a1=a,b1=-a,得an=a-a(n-1)+3(n-1)(n-2)=3n2-(9+a)n+6+2a.根据二次函数的性质及对称轴范围可求得结果;
解答:
解:(1)∵点Bn(n,bn)(n∈N*)都在斜率为6的同一条直线上,
∴
=6,即bn+1-bn=6,
于是数列{bn}是等差数列,故bn=b1+6(n-1).
∵
=(1,an+1-an),
=(-1,-bn),又
与
共线,
∴1×(-bn)-(-1)(an+1-an)=0,即an+1-an=bn,
当n≥2时,an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)
=a1+b1+b2+b3+…+bn-1
=a1+b1(n-1)+3(n-1)(n-2),
当n=1时,上式也成立.
∴an=a1+b1(n-1)+3(n-1)(n-2).
(2)把a1=a,b1=-a代入上式,
得an=a-a(n-1)+3(n-1)(n-2)=3n2-(9+a)n+6+2a.
∵12<a≤15,∴
<
≤4,
∴当n=4时,an取最小值,最小值为a4=18-2a.
∴
| bn+1-bn |
| (n+1)-n |
于是数列{bn}是等差数列,故bn=b1+6(n-1).
∵
| AnAn+1 |
| BnCn |
| AnAn+1 |
| BnCn |
∴1×(-bn)-(-1)(an+1-an)=0,即an+1-an=bn,
当n≥2时,an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)
=a1+b1+b2+b3+…+bn-1
=a1+b1(n-1)+3(n-1)(n-2),
当n=1时,上式也成立.
∴an=a1+b1(n-1)+3(n-1)(n-2).
(2)把a1=a,b1=-a代入上式,
得an=a-a(n-1)+3(n-1)(n-2)=3n2-(9+a)n+6+2a.
∵12<a≤15,∴
| 7 |
| 2 |
| 9+a |
| 6 |
∴当n=4时,an取最小值,最小值为a4=18-2a.
点评:本题考查平面向量共线的条件、向量的数量积运算、等差数列的通项公式等知识,考查学生综合运用知识解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
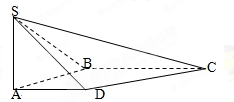 在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AD=AB=1,BC=
在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AD=AB=1,BC= 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,且PA⊥底面ABCD,BD⊥PC,E是PA的中点.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,且PA⊥底面ABCD,BD⊥PC,E是PA的中点.