题目内容
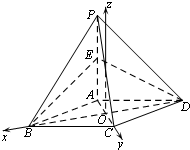
 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,且PA⊥底面ABCD,BD⊥PC,E是PA的中点.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,且PA⊥底面ABCD,BD⊥PC,E是PA的中点.(Ⅰ)求证:平面PAC⊥平面EBD;
(Ⅱ)若PA=AB=2,直线PB与平面EBD所成角的正弦值为
| 1 |
| 4 |
考点:平面与平面垂直的判定,直线与平面所成的角
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)因为PA⊥平面ABCD,所以PA⊥BD.又BD⊥PC,根据线面垂直的判定定理推断出BD⊥平面PAC,根据BD?平面EBD,进而可知平面PAC⊥平面EBD.
(Ⅱ)由(Ⅰ)可知,BD⊥AC,推断出ABCD是菱形,BC=AB=2.设AC∩BD=O,建立如图所示的坐标系O-xyz,设OB=b,OC=c,
进而表示出P,B,E,C.
,
,
.设n=(x,y,z)是面EBD的一个法向量,则n•
=n•
=0,即
取n=(0,1,c),求得BC.记直线PB与平面EBD所成的角为θ,由已知条件根据向量的数量积求得sinθ求得b和c,
进而求得四棱锥P-ABCD的体积
(Ⅱ)由(Ⅰ)可知,BD⊥AC,推断出ABCD是菱形,BC=AB=2.设AC∩BD=O,建立如图所示的坐标系O-xyz,设OB=b,OC=c,
进而表示出P,B,E,C.
| PB |
| OB |
| OE |
| OB |
| OE |
|
进而求得四棱锥P-ABCD的体积
解答:
解:(Ⅰ)∵PA⊥平面ABCD,
∴PA⊥BD.
又BD⊥PC,
∴BD⊥平面PAC,
∵BD?平面EBD,
∴平面PAC⊥平面EBD.
(Ⅱ)由(Ⅰ)可知,BD⊥AC,
∴ABCD是菱形,BC=AB=2.
设AC∩BD=O,建立如图所示的坐标系O-xyz,设OB=b,OC=c,
则P(0,-c,2),B(b,0,0),E(0,-c,1),C(0,c,0).
=(b,c,-2),
=(b,0,0),
=(0,-c,1).
设n=(x,y,z)是面EBD的一个法向量,则n•
=n•
=0,
即
取n=(0,1,c).
依题意,BC=
=2.①
记直线PB与平面EBD所成的角为θ,由已知条件
sinθ=
=
=
.②
解得b=
,c=1.
所以四棱锥P-ABCD的体积
V=
×2OB•OC•PA=
×2
×1×2=
.
∴PA⊥BD.
又BD⊥PC,
∴BD⊥平面PAC,
∵BD?平面EBD,
∴平面PAC⊥平面EBD.

(Ⅱ)由(Ⅰ)可知,BD⊥AC,
∴ABCD是菱形,BC=AB=2.
设AC∩BD=O,建立如图所示的坐标系O-xyz,设OB=b,OC=c,
则P(0,-c,2),B(b,0,0),E(0,-c,1),C(0,c,0).
| PB |
| OB |
| OE |
设n=(x,y,z)是面EBD的一个法向量,则n•
| OB |
| OE |
即
|
依题意,BC=
| b2+c2 |
记直线PB与平面EBD所成的角为θ,由已知条件
sinθ=
|n•
| ||
| |n|•|PB| |
| c | ||
|
| 1 |
| 4 |
解得b=
| 3 |
所以四棱锥P-ABCD的体积
V=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
4
| ||
| 3 |
点评:本题主要考查了线面垂直的判定定理的运用,法向量的应用等知识.注重了对学生分析问题和推理能力的考查.

练习册系列答案
相关题目
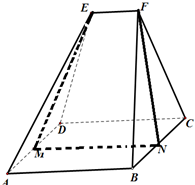 木工技艺是我国传统文化瑰宝之一,体现了劳动人民的无穷智慧.很多古代建筑和家具不用铁钉,保存到现代却依然牢固,这其中,有连接加固功能的“楔子”发挥了重要作用;如图,是一个楔子形状的直观图.其底面ABCD为一个矩形,其中AB=6,AD=4.顶部线段EF∥平面ABCD,棱EA=ED=FB=FC=6
木工技艺是我国传统文化瑰宝之一,体现了劳动人民的无穷智慧.很多古代建筑和家具不用铁钉,保存到现代却依然牢固,这其中,有连接加固功能的“楔子”发挥了重要作用;如图,是一个楔子形状的直观图.其底面ABCD为一个矩形,其中AB=6,AD=4.顶部线段EF∥平面ABCD,棱EA=ED=FB=FC=6