题目内容
(1)求椭圆25x2+16y2=400的长轴和短轴的长、离心率、焦点坐标和顶点坐标.
(2)现有6道题,其中4道甲类题,2道乙类题,张乐同学从中任取2道题解答.试求:所取的2道题都是甲类题的概率.
(2)现有6道题,其中4道甲类题,2道乙类题,张乐同学从中任取2道题解答.试求:所取的2道题都是甲类题的概率.
考点:古典概型及其概率计算公式,椭圆的简单性质
专题:圆锥曲线的定义、性质与方程,概率与统计
分析:(1)将椭圆25x2+16y2=400的方程化为标准方程,进而求出a,b,c后,可得长轴和短轴的长、离心率、焦点坐标和顶点坐标.
(2)先计算出从6个题中任取2道题的基本事件总数和2道题都是甲类题的基本事件个数,代入古典概型概率计算公式,可得答案.
(2)先计算出从6个题中任取2道题的基本事件总数和2道题都是甲类题的基本事件个数,代入古典概型概率计算公式,可得答案.
解答:
解:(1)椭圆方程化简为
+
=1
则a2=25,b2=16,c2=a2-b2=9…(1分)
长轴长:2a=10,短轴长:2b=8…(3分)
离心率:e=
=
…(4分)
焦点坐标为(0,±3)
顶点坐标为(0,±5),(±4,0)…(6分)
(2)将4道甲类题依次编号为1,2,3,4;2道乙类题依次编号为5,6.任取2道题,
基本事件为:
{1,2},{1,3},{1,4},{1,5},{1,6},
{2,3},{2,4},{2,5},{2,6},{3,4},
{3,5},{3,6},{4,5},{4,6},{5,6},共15个,
而且这些基本事件的出现是等可能的.
用A表示“都是甲类题”这一事件,
则A包含的基本事件有{1,2},{1,3},{1,4},{2,3},{2,4},{3,4},共6个,
所以P(A)=
=
…(6分)
| x2 |
| 16 |
| y2 |
| 25 |
则a2=25,b2=16,c2=a2-b2=9…(1分)
长轴长:2a=10,短轴长:2b=8…(3分)
离心率:e=
| c |
| a |
| 3 |
| 5 |
焦点坐标为(0,±3)
顶点坐标为(0,±5),(±4,0)…(6分)
(2)将4道甲类题依次编号为1,2,3,4;2道乙类题依次编号为5,6.任取2道题,
基本事件为:
{1,2},{1,3},{1,4},{1,5},{1,6},
{2,3},{2,4},{2,5},{2,6},{3,4},
{3,5},{3,6},{4,5},{4,6},{5,6},共15个,
而且这些基本事件的出现是等可能的.
用A表示“都是甲类题”这一事件,
则A包含的基本事件有{1,2},{1,3},{1,4},{2,3},{2,4},{3,4},共6个,
所以P(A)=
| 6 |
| 15 |
| 2 |
| 5 |
点评:本题考查的知识点是古典概型概率计算公式,椭圆的基本性质,其中熟练掌握利用古典概型概率计算公式求概率的步骤及椭圆的基本性质,是解答的关键.

练习册系列答案
相关题目

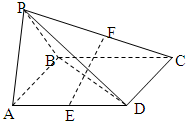 如图,四棱锥P-ABCD的底面是平行四边形,∠BAD=60°,平面PAB⊥平面ABCD,PA=PB=AB=
如图,四棱锥P-ABCD的底面是平行四边形,∠BAD=60°,平面PAB⊥平面ABCD,PA=PB=AB= 如图茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以X表示.
如图茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以X表示.