题目内容
（1）已知：a，b，x均是正数，且a＜b，求证：
＞
；
（2）证明：△ABC中，
+
+
＜2．
| a+x |
| b+x |
| a |
| b |
（2）证明：△ABC中，
| sinA |
| sinB+sinC |
| sinB |
| sinC+sinA |
| sinC |
| sinA+sinB |
考点：不等式的证明,正弦定理
专题：选作题,不等式
分析：（1）充分利用a＞b这个条件，作差，结合不等式的基本性质即可证得；
（2）应用第（1）小题结论，取倒数，得
＜
＜1由正弦定理，原题?△ABC中，求证：
+
+
＜2利用放缩法进行证明即可．
（2）应用第（1）小题结论，取倒数，得
| b |
| a |
| b+x |
| a+x |
| a |
| b+c |
| b |
| c+a |
| c |
| a+b |
解答：
证明：（1）
-
=
，
∵a，b，x均是正数，且a＜b，
∴
＞0，
∴
＞
；
（2）应用第（1）小题结论，取倒数，得
＜
＜1
由正弦定理，原题?△ABC中，求证：
+
+
＜2．
∴
＜
，
＜
，
＜
∴
+
+
＜
+
+
∴
+
+
＜2，
∴
+
+
＜2．
| a+x |
| b+x |
| a |
| b |
| (b-a)x |
| b(b+x) |
∵a，b，x均是正数，且a＜b，
∴
| (b-a)x |
| b(b+x) |
∴
| a+x |
| b+x |
| a |
| b |
（2）应用第（1）小题结论，取倒数，得
| b |
| a |
| b+x |
| a+x |
由正弦定理，原题?△ABC中，求证：
| a |
| b+c |
| b |
| c+a |
| c |
| a+b |
∴
| a |
| b+c |
| 2a |
| a+b+c |
| b |
| c+a |
| 2b |
| a+b+c |
| c |
| a+b |
| 2c |
| a+b+c |
∴
| a |
| b+c |
| b |
| c+a |
| c |
| a+b |
| 2a |
| a+b+c |
| 2b |
| a+b+c |
| 2c |
| a+b+c |
∴
| a |
| b+c |
| b |
| c+a |
| c |
| a+b |
∴
| sinA |
| sinB+sinC |
| sinB |
| sinC+sinA |
| sinC |
| sinA+sinB |
点评：本题主要考查了不等式的证明、放缩法和类比思想，在证明不等式的时候，在直接证明遇到困难的时候，可以利用不等式的传递性，把要证明的不等式加强为一个易证的不等式，即欲证A＞B，我们可以适当的找一个中间量C作为媒介，证明A＞C且C＞B，从而得到A＞B．我们把这种把B放大到C（或把A缩小到C）的方法称为放缩法．
练习册系列答案
相关题目
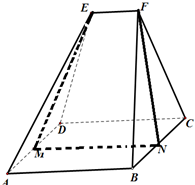木工技艺是我国传统文化瑰宝之一，体现了劳动人民的无穷智慧．很多古代建筑和家具不用铁钉，保存到现代却依然牢固，这其中，有连接加固功能的“楔子”发挥了重要作用；如图，是一个楔子形状的直观图．其底面ABCD为一个矩形，其中AB=6，AD=4．顶部线段EF∥平面ABCD，棱EA=ED=FB=FC=6
