题目内容
学校在高二开设了当代战争风云、投资理财、汽车模拟驾驶与保养、硬笔书法共4门选修课,每个学生必须且只需从4门选修课中任选1门选修课选修,对于该年级的甲、乙、丙3名学生:求:
(1)甲选战争风云课而且乙选投资理财课的概率;
(2)这3名学生选择的选修课互不相同的概率;
(3)投资理财选修课被这3名学生选择的人数X的分布列.
(1)甲选战争风云课而且乙选投资理财课的概率;
(2)这3名学生选择的选修课互不相同的概率;
(3)投资理财选修课被这3名学生选择的人数X的分布列.
考点:离散型随机变量的期望与方差,相互独立事件的概率乘法公式
专题:应用题,概率与统计
分析:(1)利用相互独立事件的概率公式求解即可;
(2)3名学生选择的选修课互不相同的概率P1=
=
.
(3)设某一选修课被这3名学生选择的人数为ζ,则ζ=0,1,2,3.分别求出其概率,由此能求出ζ的分布列和数学期望.
(2)3名学生选择的选修课互不相同的概率P1=
| ||
| 43 |
| 3 |
| 8 |
(3)设某一选修课被这3名学生选择的人数为ζ,则ζ=0,1,2,3.分别求出其概率,由此能求出ζ的分布列和数学期望.
解答:
解:(1)记甲选战争风云课为事件A、乙选投资理财课为事件B,
由于事件A,B相互独立,且P(A)=
,P(B)=
.-----------(2分)
故甲选战争风云课、乙选投资理财课的概率为P(A?B)=P(A)?P(B)=
.--------(3分)
(2)3名学生选择了3门不同的选修课的概率为P1=
=
----------(6分)
(3)设投资理财选修课被这3名学生选择的人数为ζ,则ζ═0,1,2,3----(7分)
P(ζ=0)=
=
;P(ζ=1)=
=
;
P(ζ=2)=
=
;P(ζ=3)=
=
-----------(11分)
X的分布列为
-----------(12分)
由于事件A,B相互独立,且P(A)=
| 1 |
| 4 |
| 1 |
| 4 |
故甲选战争风云课、乙选投资理财课的概率为P(A?B)=P(A)?P(B)=
| 1 |
| 16 |
(2)3名学生选择了3门不同的选修课的概率为P1=
| ||
| 43 |
| 3 |
| 8 |
(3)设投资理财选修课被这3名学生选择的人数为ζ,则ζ═0,1,2,3----(7分)
P(ζ=0)=
| 33 |
| 43 |
| 27 |
| 64 |
| ||
| 43 |
| 27 |
| 64 |
P(ζ=2)=
3•
| ||
| 43 |
| 9 |
| 64 |
| ||
| 43 |
| 1 |
| 64 |
X的分布列为
| ζ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
点评:本题考查概率的计算,考查离散型随机变量的分布列和数学期望,解题时要认真审题,仔细解答,注意概率知识的灵活运用.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
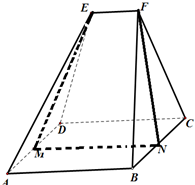 木工技艺是我国传统文化瑰宝之一,体现了劳动人民的无穷智慧.很多古代建筑和家具不用铁钉,保存到现代却依然牢固,这其中,有连接加固功能的“楔子”发挥了重要作用;如图,是一个楔子形状的直观图.其底面ABCD为一个矩形,其中AB=6,AD=4.顶部线段EF∥平面ABCD,棱EA=ED=FB=FC=6
木工技艺是我国传统文化瑰宝之一,体现了劳动人民的无穷智慧.很多古代建筑和家具不用铁钉,保存到现代却依然牢固,这其中,有连接加固功能的“楔子”发挥了重要作用;如图,是一个楔子形状的直观图.其底面ABCD为一个矩形,其中AB=6,AD=4.顶部线段EF∥平面ABCD,棱EA=ED=FB=FC=6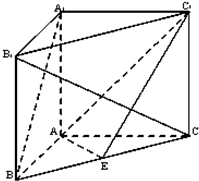 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1,且E是BC中点.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1,且E是BC中点.