题目内容

如图，在平行四边形ABCD中，M为CD中点，若
AC
=λ
AM
+μ
AB
．则μ的值为（　　）
A、
1
4
B、
1
3
C、
1
2
D、1
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：在平行四边形ABCD中，M为CD中点，可得
AM
=
AD
+
DM
=
AD
+
1
2
AB
，代入
AC
=λ
AM
+μ
AB
，可得
AC
=λ
AD
+(
1
2
λ+μ)
AB
，与
AC
=
AD
+
AB
比较即可得出．
解答： 解：∵在平行四边形ABCD中，M为CD中点，
∴
AM
=
AD
+
DM
=
AD
+
1
2
AB
，
∵
AC
=λ
AM
+μ
AB
，
∴
AC
=λ(
AD
+
1
2
AB
)+μ
AB

=λ
AD
+(
1
2
λ+μ)
AB
，
又
AC
=
AD
+
AB
，
∴λ=1，
1
2
λ+μ=1，
解得μ=
1
2
．
故选：C．
点评：本题考查了向量的三角形法则、平行四边形法则、向量基本定理，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
在平行四边形ABCD中，对角线AC与BD交于点O，若
AB
+
AD
=λ
AO
，则实数λ等于（　　）
A、4B、3C、2D、1
若函数f（x）满足：（Ⅰ）函数f（x）的定义域是R；（Ⅱ）对任意x1，x2∈R，有f（x1+x2）+f（x1-x2）=2f（x1）f（x2）；（Ⅲ）f（1）=
3
2
，则下列命题正确的是
 
（只写出所有正确命题的序号）
①函数f（x）是奇函数；
②函数f（x）是偶函数；
③对任意n1，n2∈N，若n1＜n2，则f（n1）＜f（n2）；
④对任意x∈R，有f（x）≥-1．
曲线y=x2-3x在点P处的切线平行于x轴，则点P的坐标为
 
．
请编写一个程序，求满足m+n＜10的所有正整数对．
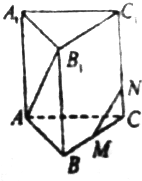正三棱柱ABC-A1B1C1的侧棱长为2，底面边长为1，点M是BC的中点．
（1）在直线CC1上求一点N，使MN⊥AB1；
（2）求cos＜
BA1
，
CB1
＞
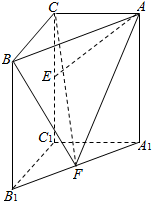如图，在直三棱柱ABC-A1B1C1中，∠BCA=90°，AC=BC=AA1=2，E，F分别是CC1，A1B1的中点．
（1）求证：AE⊥平面BCF；
（2）求点F到平面ABE的距离．
已知
a
=（2，-1），
b
=（-1，3），
c
=（7，-11），且
c
=x
a
-y
b
，求实数x，y的值．
已知sinα=
4
5
，cos（α+β）=-
3
5
．α、β均为锐角，求sinβ，cosβ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网