题目内容
求下列函数定义域.
(1)y=(1+sinx)2;
(2)y=ln
;
(3)y=xe1-cosx;
(4)y=
;
(5)y=x
.
(1)y=(1+sinx)2;
(2)y=ln
| x2+1 |
(3)y=xe1-cosx;
(4)y=
| 1 |
| (1-3x)4 |
(5)y=x
| 1+x2 |
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:(1)不论x取何值,函数表达式(1+sinx)2都有意义,故函数的定义域易求;
(2)要使函数有意义,x应满足
,解得x即可;
(3)不论x取何值,函数表达式xe1-cosx都有意义);
(4)要使函数有意义,x应满足1-3x≠0,解得x≠
,解得x即可;
(5)要使函数有意义,x应满足1+x2≥0,解得x∈R,故函数的定义域也可求.
(2)要使函数有意义,x应满足
|
(3)不论x取何值,函数表达式xe1-cosx都有意义);
(4)要使函数有意义,x应满足1-3x≠0,解得x≠
| 1 |
| 3 |
(5)要使函数有意义,x应满足1+x2≥0,解得x∈R,故函数的定义域也可求.
解答:
解:(1)不论x取何值,函数表达式(1+sinx)2都有意义,故函数的定义域为(-∞,+∞);
(2)要使函数有意义,x应满足
,解得x∈R,故函数的定义域为(-∞,+∞);
(3)不论x取何值,函数表达式xe1-cosx都有意义,故函数的定义域为(-∞,+∞);
(4)要使函数有意义,x应满足1-3x≠0,解得x≠
,故函数的定义域为(-∞,
)∪(
,+∞);
(5)要使函数有意义,x应满足1+x2≥0,解得x∈R,故函数的定义域为(-∞,+∞);
(2)要使函数有意义,x应满足
|
(3)不论x取何值,函数表达式xe1-cosx都有意义,故函数的定义域为(-∞,+∞);
(4)要使函数有意义,x应满足1-3x≠0,解得x≠
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
(5)要使函数有意义,x应满足1+x2≥0,解得x∈R,故函数的定义域为(-∞,+∞);
点评:函数的定义域是使函数的表达式有意义的x的取值范围,主要使对数的真数为正数,分母不为0,开偶次方根是被开方数大于等于0即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数y=sin(2x+φ)在(
,
)上单调递增,其中φ∈(π,2π),则φ的取值范围为( )
| π |
| 4 |
| π |
| 3 |
A、[
| ||||
B、(π,
| ||||
C、[
| ||||
D、[
|
函数f(x)=lg(|x|+1)-sin2x的零点个数为( )
| A、9 | B、10 | C、11 | D、12 |
在平行四边形ABCD中,对角线AC与BD交于点O,若
+
=λ
,则实数λ等于( )
| AB |
| AD |
| AO |
| A、4 | B、3 | C、2 | D、1 |
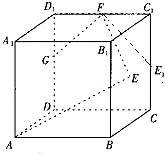 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E是正方形BCC1B1的中心,点F,G分别是棱C1D1,DD1的中点.设点E1是点E在平面DCC1D1内的正投影.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E是正方形BCC1B1的中心,点F,G分别是棱C1D1,DD1的中点.设点E1是点E在平面DCC1D1内的正投影.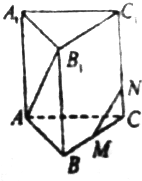 正三棱柱ABC-A1B1C1的侧棱长为2,底面边长为1,点M是BC的中点.
正三棱柱ABC-A1B1C1的侧棱长为2,底面边长为1,点M是BC的中点.