题目内容
已知函数f(x)=loga(x+1)与g(x)=loga(-x+1)(a>0且a≠1).
(1)若函数f(x)=loga(x+1)过点(7,3),求g(
)的值;
(2)当0<a<1时,解不等式2f(x)≥g(x).
(1)若函数f(x)=loga(x+1)过点(7,3),求g(
| 7 |
| 8 |
(2)当0<a<1时,解不等式2f(x)≥g(x).
考点:对数函数图象与性质的综合应用
专题:函数的性质及应用
分析:(1)根据函数f(x)过点(7,3),便说明该点满足函数解析式,所以带入解析式便可求出a.从而求出g(x),然后将
代入g(x)便求得g(
).
(2)把f(x),g(x)带入不等式2f(x)≥g(x),在根据对数函数在0<a<1时的单调性得到不等式
≤3,为使函数f(x),g(x)有意义,再限制x:x+1>0,且-x+1>0,解这几个不等式,便得到原不等式的解.
| 7 |
| 8 |
| 7 |
| 8 |
(2)把f(x),g(x)带入不等式2f(x)≥g(x),在根据对数函数在0<a<1时的单调性得到不等式
| (x+1)2 |
| -x+1 |
解答:
解:(1)由题意得:3=loga8,
∴a3=8,∴a=2;
∴g(
)=log2(-
+1)=log22-3=-3.
(2)解不等式2f(x)≥g(x),
即解2loga(x+1)≥loga(-x+1),即解loga(x+1)2≥loga(-x+1);
∵0<a<1,∴对数函数y=logax是减函数;
∴由loga(x+1)2≥loga(-x+1)得
;
解得:-1<x≤0;
∴不等式的解集是(-1,0].
∴a3=8,∴a=2;
∴g(
| 7 |
| 8 |
| 7 |
| 8 |
(2)解不等式2f(x)≥g(x),
即解2loga(x+1)≥loga(-x+1),即解loga(x+1)2≥loga(-x+1);
∵0<a<1,∴对数函数y=logax是减函数;
∴由loga(x+1)2≥loga(-x+1)得
|
解得:-1<x≤0;
∴不等式的解集是(-1,0].
点评:理解函数曲线上的点的坐标与函数解析式的关系,第二问解不等式时,别忘了限制x使函数f(x),g(x)有意义.

练习册系列答案
相关题目
 如图,正方体ABCD-A1B1C1D1中,已知E为棱CC1上的动点.
如图,正方体ABCD-A1B1C1D1中,已知E为棱CC1上的动点.
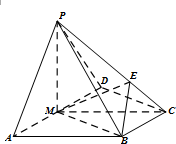 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,底面ABCD是直角梯形,AD∥BC,∠ADC=90°,AD=2BC=2,CD=
如图,在四棱锥P-ABCD中,侧面PAD是正三角形,底面ABCD是直角梯形,AD∥BC,∠ADC=90°,AD=2BC=2,CD=