题目内容
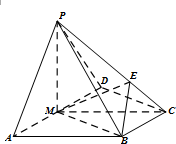如图，在四棱锥P-ABCD中，侧面PAD是正三角形，底面ABCD是直角梯形，AD∥BC，∠ADC=90°，AD=2BC=2，CD=| 3 |
（1）求证：平面EBM⊥平面PAD；
（2）若∠MEC=90°，求三棱锥A-BME的体积．
考点：棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题：综合题,空间位置关系与距离
分析：（1）证明MBCD为平行四边形，进而证明BM⊥AD，利用平面PAD⊥平面ABCD，可得BM⊥面PAD，即可证明平面EBM⊥平面PAD；
（2）利用VA-BME=VE-ABM，即可求三棱锥A-BME的体积．
（2）利用VA-BME=VE-ABM，即可求三棱锥A-BME的体积．
解答：
（1）证明：∵M是AD的中点且AD=2，∴MD=1，
又∵AD∥BC，BC=1，
∴MBCD为平行四边形，
∵∠ADC=90°，DC∥MB，
∴∠AMB=90°即BM⊥AD，
∵平面PAD⊥平面ABCD，BM?平面ABCD，
∴BM⊥面PAD，∴平面EBM⊥面PAD（4分）
（2）解：∵AM=1，BM=3且BM⊥AM，
∴S△ABM=
．
过E做EG∥PM交MC于G，则
∵PM⊥平面ABCD，∴EG⊥平面ABCD，
∴EG为三棱锥E-AMB的高，
在直角三角形PMC中：PM=
，MC=2
又ME⊥PC，∴ME=
，EC=
，
∴EG=
（10分）
∴VA=BME=VE-ABM=
×
×
=
（12分）
又∵AD∥BC，BC=1，
∴MBCD为平行四边形，
∵∠ADC=90°，DC∥MB，
∴∠AMB=90°即BM⊥AD，
∵平面PAD⊥平面ABCD，BM?平面ABCD，
∴BM⊥面PAD，∴平面EBM⊥面PAD（4分）
（2）解：∵AM=1，BM=3且BM⊥AM，
∴S△ABM=
| ||
| 2 |
过E做EG∥PM交MC于G，则
∵PM⊥平面ABCD，∴EG⊥平面ABCD，
∴EG为三棱锥E-AMB的高，
在直角三角形PMC中：PM=
| 3 |
又ME⊥PC，∴ME=
2
| ||
| 7 |
| 4 | ||
|
∴EG=
4
| ||
| 7 |
∴VA=BME=VE-ABM=
| 1 |
| 3 |
4
| ||
| 7 |
| ||
| 2 |
| 2 |
| 7 |
点评：本题考查平面与平面垂直的判定与性质，考查锥体体积的计算，正确运用平面与平面垂直的判定与性质，转换底面求体积是关键．
练习册系列答案
相关题目
