题目内容
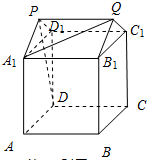
已知几何体由正方体和直三棱柱组成，其三视图和直观图（单位：cm）如图所示．设两条异面直线A1Q和PD所成的角为θ，求cosθ的值．
考点：异面直线及其所成的角
专题：空间角
分析：由PQ∥CD，且PQ=CD，知PD∥QC，得∠A1QC为异面直线A1Q、PD所成的角（或其补角）．由此能求出两条异面直线A1Q和PD所成的角的大小．
解答：
解：由PQ∥CD，且PQ=CD，知PD∥QC，
故∠A1QC为异面直线A1Q、PD所成的角（或其补角）．
由题设知A1Q2=A1
+B1Q2=22+
2=6，
A1C=
×2=2
，
取BC中点E，则QE⊥BC，且QE=3，
QC2=QE2+EC2=32+12=10．
由余弦定理，
得cosθ=cos∠A1QC=
=
=
．
∴两条异面直线A1Q和PD所成的角θ=arccos
．
解：由PQ∥CD，且PQ=CD，知PD∥QC，故∠A1QC为异面直线A1Q、PD所成的角（或其补角）．
由题设知A1Q2=A1
| B | 2 1 |
| 2 |
A1C=
| 3 |
| 3 |
取BC中点E，则QE⊥BC，且QE=3，
QC2=QE2+EC2=32+12=10．
由余弦定理，
得cosθ=cos∠A1QC=
| A1Q2+QC2-A1C2 |
| 2A1Q•QC |
=
| 6+10-12 | ||||
2
|
| ||
| 15 |
∴两条异面直线A1Q和PD所成的角θ=arccos
| ||
| 15 |
点评：本题考查两条异面直线所成角的大小的标法，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
