题目内容
如图，设区域D={x（x，y）|0≤x≤π，0≤y≤1}，向区域D内随机投入一点，且投入到区域内任一点都是等可能的，则点落入到阴影区M={（x，y）|0≤x≤π，0≤y≤sinx}的概率为（ ）| A、1 | ||
B、
| ||
C、
| ||
D、
|
考点：几何概型
专题：计算题,概率与统计
分析：根据积分求解出阴影部分的面积，然后再求解区域D的面积，再将它们代入几何概型计算公式计算出概率．
解答：
解：阴影部分面积S=∫0π（sinx）dx=（-cosx）|0π=-cosπ+cos0=2
区域D={x（x，y）|0≤x≤π，0≤y≤1}的面积S′=π
∴所投的点落在阴影部分的概率P=
．
故选：C．
区域D={x（x，y）|0≤x≤π，0≤y≤1}的面积S′=π
∴所投的点落在阴影部分的概率P=
| 2 |
| π |
故选：C．
点评：本题考查几何概型的概率，可以为长度、面积、体积等，而且这个“几何度量”只与“大小”有关，而与形状和位置无关．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
设i为虚数单位，复数z的共轭复数为
，且（
-1）（1+i）=2i，则复数z的模为（ ）
. |
| z |
. |
| z |
| A、5 | ||
B、
| ||
| C、2-i | ||
| D、1 |
设函数f（x）（x∈R）满足f（-x）=f（x），f（x）=f（2-x），且当x∈[0，1]时，f（x）=x3．又函数g（x）=|cos（πx）|，则函数h（x）=g（x）-f（x）在[-
，
]上的零点个数为（ ）
| 1 |
| 2 |
| 3 |
| 2 |
| A、5 | B、6 | C、7 | D、8 |
将并排的有不同编号的5个房间安排给5个工作人员临时休息，假定每个人可以选择任意房间，且选择各个房间是等可能的，则恰有两个房间无人选择的安排方式的总数为（ ）
| A、900 | B、1500 |
| C、1800 | D、1440 |
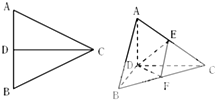已知正△ABC的边长为a，CD是AB边上的高，E、F分别是AC和BC边的中点，现将△ABC沿CD翻折成直二面角A-DC-B，如图所示．
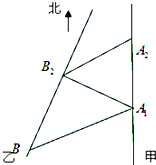如图，甲船以每小时15