题目内容
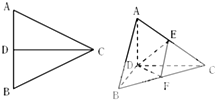 已知正△ABC的边长为a,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图所示.
已知正△ABC的边长为a,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图所示.(Ⅰ)试判断折叠后直线AB与平面DEF的位置关系,并说明理由;
(Ⅱ)若棱锥E-DFC的体积为
| ||
| 24 |
(Ⅲ)在线段AC上是否存在一点P,使BP⊥DF?如果存在,求出
| AP |
| AC |
考点:与二面角有关的立体几何综合题,棱柱、棱锥、棱台的体积,直线与平面所成的角
专题:空间位置关系与距离
分析:(Ⅰ)由已知条件推导出EF∥AB,由此能证明AB∥平面DEF.
(Ⅱ)将△ABC沿CD翻折成直二面角A-DC-B,AD⊥BD,AD⊥平面BCD,取CD中点M,则EM∥AD,EM⊥平面BCD,且EM=
,由此利用棱锥的体积能求出a.
(Ⅲ)线段AC上存在一点P,使BP⊥DF.三角形BDF为正三角形,过B做BK⊥DF,延长BK交DC于K,过K做KP∥DA,交AC于P.则点P即为所求.利用空间几何知识能进行证明.
(Ⅱ)将△ABC沿CD翻折成直二面角A-DC-B,AD⊥BD,AD⊥平面BCD,取CD中点M,则EM∥AD,EM⊥平面BCD,且EM=
| a |
| 2 |
(Ⅲ)线段AC上存在一点P,使BP⊥DF.三角形BDF为正三角形,过B做BK⊥DF,延长BK交DC于K,过K做KP∥DA,交AC于P.则点P即为所求.利用空间几何知识能进行证明.
解答:
解:(Ⅰ)AB∥平面DEF,
如图.在△ABC中,∵E,F分别是AC,BC的中点,∴EF∥AB,
又AB不包含于平面DEF,EF?平面DEF,
∴AB∥平面DEF.…(4分)
(Ⅱ)∵AD⊥CD,BD⊥CD,将△ABC沿CD翻折成直二面角A-DC-B,
∴AD⊥BD,AD⊥平面BCD,取CD中点M,则EM∥AD,
∴EM⊥平面BCD,且EM=
,
∵棱锥E-DFC的体积为
,
∴V=
×
×
=
,解得a=2.…(8分)
(Ⅲ)线段AC上存在一点P,使BP⊥DF.
三角形BDF为正三角形,过B做BK⊥DF,
延长BK交DC于K,过K做KP∥DA,交AC于P.则点P即为所求.
证明:∵AD⊥平面BCD,KP∥DA,
∴PK⊥平面BCD,PK⊥DF,又 BK⊥DF,PK∩BK=K,
∴DF⊥平面PKB,DF⊥PB.又∠DBK=∠KBC=∠BCK=30°,∴DK=KF=KC/2.
故AP:OC=1:2,AP:AC=1:3 …(12分)
如图.在△ABC中,∵E,F分别是AC,BC的中点,∴EF∥AB,

又AB不包含于平面DEF,EF?平面DEF,
∴AB∥平面DEF.…(4分)
(Ⅱ)∵AD⊥CD,BD⊥CD,将△ABC沿CD翻折成直二面角A-DC-B,
∴AD⊥BD,AD⊥平面BCD,取CD中点M,则EM∥AD,
∴EM⊥平面BCD,且EM=
| a |
| 2 |
∵棱锥E-DFC的体积为
| ||
| 24 |
∴V=
| 1 |
| 3 |
| a |
| 4 |
| ||
| 16 |
| ||
| 24 |
(Ⅲ)线段AC上存在一点P,使BP⊥DF.
三角形BDF为正三角形,过B做BK⊥DF,
延长BK交DC于K,过K做KP∥DA,交AC于P.则点P即为所求.
证明:∵AD⊥平面BCD,KP∥DA,
∴PK⊥平面BCD,PK⊥DF,又 BK⊥DF,PK∩BK=K,
∴DF⊥平面PKB,DF⊥PB.又∠DBK=∠KBC=∠BCK=30°,∴DK=KF=KC/2.
故AP:OC=1:2,AP:AC=1:3 …(12分)
点评:本题考查直线与平面的位置关系的判断与证明,考查实数的求法,考查满足条件的点的判断与求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
在复平面内,复数z=(
-1)+(2x-1)i的对应点位于第二象限,则实数x的范围是( )
| x |
| A、(1,+∞) |
| B、(-∞,0) |
| C、(0,1) |
| D、(-∞,0)∪(1,+∞) |
若A={x|y=log2(x-2)},B={y|y=|x|},则A∩B=( )
| A、(0,+∞) |
| B、[0,+∞) |
| C、(2,+∞) |
| D、[0,2) |

 如图,设区域D={x(x,y)|0≤x≤π,0≤y≤1},向区域D内随机投入一点,且投入到区域内任一点都是等可能的,则点落入到阴影区M={(x,y)|0≤x≤π,0≤y≤sinx}的概率为( )
如图,设区域D={x(x,y)|0≤x≤π,0≤y≤1},向区域D内随机投入一点,且投入到区域内任一点都是等可能的,则点落入到阴影区M={(x,y)|0≤x≤π,0≤y≤sinx}的概率为( ) 已知椭圆C:
已知椭圆C: