Question

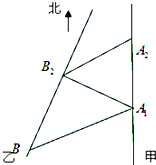如图，甲船以每小时15

2

海里的速度向正北方航行，乙船按固定方向匀速直线航行，当甲船位于A₁处时，乙船位于甲船的南偏西75°方向的B₁处，此时两船相距20海里，当甲船航行40分钟到达A₂处时，乙船航行到甲船的南偏西45°方向的B₂处，此时两船相距10海里，问乙船每小时航行多少海里？

Answer 1

考点：解三角形的实际应用

专题：应用题,解三角形

分析：在△A₁A₂B₂中，由余弦定理得A₁B₂，在△A₁B₁B₂中，由余弦定理得B₁B₂，即可求出乙船的速度．

解答： 解：由已知得A₁B₁=20，A1A2=10

2

，A₂B₂=10，∠A1A2B2=45o，
在△A₁A₂B₂中，由余弦定理得：A1B22=(10

2

)2+102-2•10

2

•10•

2

2

=100，∴A₁B₂=10，…（4分）
又A₂B₂=A₁B₂，得∠A2A1B2=45o，∠B₂A₁B₁=180°-75°-45°=60°，…（6分）
又在△A₁B₁B₂中，由余弦定理得：B1B22=400+100-2•20•10•

1

2

=300，∴B1B2=10

3

，…（10分）
则乙船的速度v=

10 3

40

×60=15

3

（海里）
答：乙船每小时航行15

3

海里．  …（12分）

点评：本题考查解三角形的实际应用，考查余弦定理，考查学生的计算能力，属于中档题．