题目内容
设函数f(x)(x∈R)满足f(-x)=f(x),f(x)=f(2-x),且当x∈[0,1]时,f(x)=x3.又函数g(x)=|cos(πx)|,则函数h(x)=g(x)-f(x)在[-
,
]上的零点个数为( )
| 1 |
| 2 |
| 3 |
| 2 |
| A、5 | B、6 | C、7 | D、8 |
考点:函数零点的判定定理
专题:数形结合法
分析:本题应该采用图解法,在同一坐标系内画出函数在[-
,
]上图象交点的个数既是h(x)零点的个数.
| 1 |
| 2 |
| 3 |
| 2 |
解答:
解:∵f(-x)=f(x),∴f(x)是偶函数
∵f(x)=f(2-x)
∴f(-x+2)=f(-x)
∴f(x)=f(x+2)
∴f(x)是周期函数,周期为2
∵当x∈[0,1]时,f(x)=x3
∴当x∈[-1,0]]时,f(x)=-x3
∴x∈[1,
]时,f(x)=f(x-2)=-(x-2)3
对于g(x)=|cos(πx)|
∵g(-x)=g(x),
∴g(x)是偶函数
当x∈[-
,
],πx∈[-
,
],
∴cosπx>0,
∴g(x)=cos(πx),
当x∈[
,
],πx∈[
,
],
∴cosπx<0,
∴g(x)=-cos(πx)
在同一坐标系内画出函数f(x)和g(x)在[-
,
]上的简图,如图示:
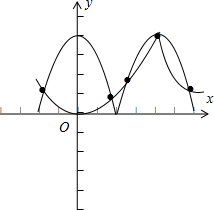
观察交点个数为5个
∴h(x)=g(x)-f(x)在[-
,
]上的零
点个数有5个.
故答案为:A.
∵f(x)=f(2-x)
∴f(-x+2)=f(-x)
∴f(x)=f(x+2)
∴f(x)是周期函数,周期为2
∵当x∈[0,1]时,f(x)=x3
∴当x∈[-1,0]]时,f(x)=-x3
∴x∈[1,
| 3 |
| 2 |
对于g(x)=|cos(πx)|
∵g(-x)=g(x),
∴g(x)是偶函数
当x∈[-
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
| π |
| 2 |
∴cosπx>0,
∴g(x)=cos(πx),
当x∈[
| 1 |
| 2 |
| 3 |
| 2 |
| π |
| 2 |
| 3π |
| 2 |
∴cosπx<0,
∴g(x)=-cos(πx)
在同一坐标系内画出函数f(x)和g(x)在[-
| 1 |
| 2 |
| 3 |
| 2 |

观察交点个数为5个
∴h(x)=g(x)-f(x)在[-
| 1 |
| 2 |
| 3 |
| 2 |
点个数有5个.
故答案为:A.
点评:本题考察了函数的零点的个数,转化为求函数交点的个数,采用了转化和数形结合思想.

练习册系列答案
相关题目
已知a>1,logax<logay<0,则( )
| A、1<x<y |
| B、1<y<x |
| C、0<x<y<1 |
| D、0<y<x<1 |
在复平面内,复数z=(
-1)+(2x-1)i的对应点位于第二象限,则实数x的范围是( )
| x |
| A、(1,+∞) |
| B、(-∞,0) |
| C、(0,1) |
| D、(-∞,0)∪(1,+∞) |
3名男生3名女生站成两排照相,要求每排3人且3名男生不在同一排,则不同的站法有( )
| A、324种 | B、360种 |
| C、648种 | D、684种 |
若A={x|y=log2(x-2)},B={y|y=|x|},则A∩B=( )
| A、(0,+∞) |
| B、[0,+∞) |
| C、(2,+∞) |
| D、[0,2) |
 如图,设区域D={x(x,y)|0≤x≤π,0≤y≤1},向区域D内随机投入一点,且投入到区域内任一点都是等可能的,则点落入到阴影区M={(x,y)|0≤x≤π,0≤y≤sinx}的概率为( )
如图,设区域D={x(x,y)|0≤x≤π,0≤y≤1},向区域D内随机投入一点,且投入到区域内任一点都是等可能的,则点落入到阴影区M={(x,y)|0≤x≤π,0≤y≤sinx}的概率为( )